पारस्परिक या पारस्परिक सभी प्रकार के बीजीय समीकरणों में बहुत उपयोगी है। उदाहरण के लिए, जब आप एक भिन्न को दूसरी भिन्न से विभाजित करते हैं, तो आप पहली भिन्न को दूसरी के व्युत्क्रम से गुणा करते हैं। किसी रेखा के समीकरण की तलाश करते समय आपको व्युत्क्रम का उपयोग करने की भी आवश्यकता होती है।
कदम
विधि 1 का 3: भिन्न या पूर्णांक का व्युत्क्रम ज्ञात करना
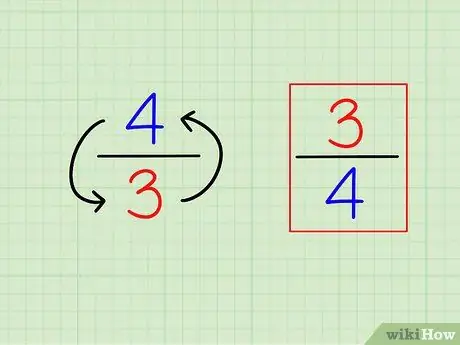
चरण 1. भिन्न को उल्टा करके उसका व्युत्क्रम ज्ञात कीजिए।
"पारस्परिक" या विपरीत की परिभाषा बहुत आसान है। किसी भी पूर्णांक का व्युत्क्रम ज्ञात करने के लिए, बस "1 (वह संख्या)" की गणना करें। भिन्नों के लिए, व्युत्क्रम भिन्न भिन्न होता है, अर्थात संख्याएँ "उल्टे" (उलटा) होती हैं।
- उदाहरण के लिए, के विपरीत 3/4 है 4/3.
- कोई भी संख्या जब उसके पारस्परिक रिटर्न से गुणा किया जाता है 1.
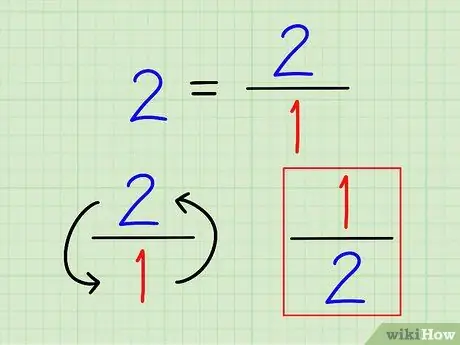
चरण 2. पूर्ण संख्या के व्युत्क्रम को भिन्न के रूप में लिखिए।
फिर से, किसी संख्या का व्युत्क्रम हमेशा 1 (वह संख्या) होता है। पूर्ण संख्याओं के लिए, उन्हें भिन्नों के रूप में लिखें। उस संख्या को दशमलव में परिकलित करने का कोई मतलब नहीं है।
उदाहरण के लिए, 2 का व्युत्क्रम 1 2 =. है 1/2.
विधि 2 का 3: मिश्रित भिन्न का प्रतिलोम ज्ञात करना

चरण 1. मिश्रित संख्याओं को पहचानें।
मिश्रित भिन्नों में पूर्ण संख्याएँ और भिन्न होते हैं, जैसे कि 24/5. एक मिश्रित संख्या का व्युत्क्रम ज्ञात करने के दो चरण हैं जैसा कि नीचे वर्णित है।

चरण 2. मिश्रित संख्याओं को अनुचित भिन्नों में बदलें।
याद रखें कि 1 को हमेशा (संख्या)/(एक ही संख्या) के रूप में लिखा जा सकता है, और समान हर (निचली संख्या) वाली भिन्नों को एक साथ जोड़ा जा सकता है। यहाँ 2. का उपयोग करके एक उदाहरण दिया गया है4/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
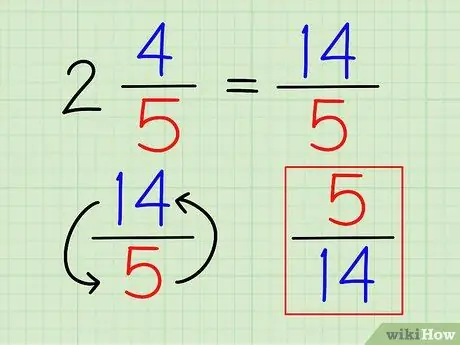
चरण 3. भिन्न को पलटें।
एक बार जब संख्या पूरी तरह से भिन्न के रूप में लिखी जाती है, तो आप भिन्न को उलट कर, किसी अन्य भिन्न की तरह इसका व्युत्क्रम ज्ञात कर सकते हैं।
उपरोक्त उदाहरण में, का व्युत्क्रम 14/5 है 5/14.
विधि 3 का 3: दशमलव के विपरीत ढूँढना
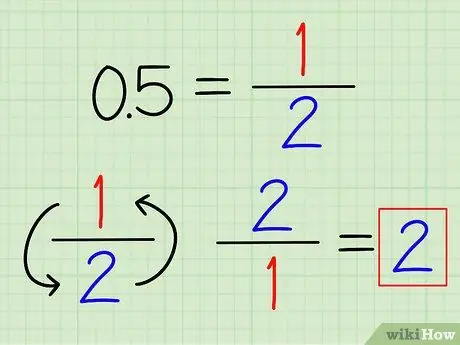
चरण 1. यदि संभव हो तो दशमलव को भिन्नों में बदलें।
आप अक्सर उपयोग की जाने वाली कुछ दशमलव संख्याओं को पहचान सकते हैं, जिन्हें आसानी से भिन्नों में परिवर्तित किया जा सकता है। उदाहरण के लिए, 0.5 = 1/2 और 0.25 = 1/4. एक बार जब दशमलव को भिन्न में बदल दिया जाता है, तो इसके पारस्परिक को खोजने के लिए बस भिन्न को पलटें।
उदाहरण के लिए, 0.5 का व्युत्क्रम है 2/1 = 2.

चरण 2. एक विभाजन समस्या लिखें।
यदि आप इसे भिन्न में नहीं बदल सकते हैं, तो विभाजन समस्या के रूप में संख्या के पारस्परिक की गणना करें: 1 (दशमलव)। आप इसे हल करने के लिए कैलकुलेटर का उपयोग कर सकते हैं या इसे मैन्युअल रूप से हल करने के लिए अगले चरण पर जा सकते हैं।
उदाहरण के लिए, आप 1 0.4 की गणना करके 0.4 का व्युत्क्रम ज्ञात कर सकते हैं।

चरण 3. भाग के प्रश्न को पूर्ण संख्याओं का उपयोग करने के लिए बदलें।
दशमलव को विभाजित करने का पहला चरण दशमलव बिंदु को तब तक खिसकाना है जब तक कि सभी संख्याएँ पूर्ण संख्याएँ न हो जाएँ। जब तक आप दोनों संख्याओं के दशमलव बिंदु को समान चरणों से आगे बढ़ाते हैं, आपको सही उत्तर मिलेगा।
उदाहरण के लिए, आप 1 0, 4 का उपयोग कर सकते हैं और इसे 10 4 के रूप में फिर से लिख सकते हैं। इस स्थिति में, आप सभी दशमलव स्थानों को एक कदम दाईं ओर ले जाते हैं, उसी तरह आप प्रत्येक संख्या को दस से गुणा करते हैं।

चरण 4. लंबे विभाजन का उपयोग करके समस्या को हल करें।
व्युत्क्रम की गणना के लिए लंबी विभाजन विधि का उपयोग करें। अगर आप १० ४ गिनेंगे तो आपको जवाब मिल जाएगा 2, 5 जो 0, 4 का व्युत्क्रम है।
टिप्स
- किसी संख्या का ऋणात्मक व्युत्क्रम नियमित व्युत्क्रम के समान होता है, जिसमें इसे ऋणात्मक से गुणा किया जाता है। उदाहरण के लिए, का ऋणात्मक व्युत्क्रम 3/4 है -4/3.
- पारस्परिक या पारस्परिक को अक्सर "गुणा व्युत्क्रम" के रूप में जाना जाता है।
- संख्या 1 स्वयं के विपरीत है क्योंकि 1 1 = 1.
- संख्या 0 का कोई व्युत्क्रम नहीं है क्योंकि 0 अपरिभाषित है।







