यदि आप पहले ही समझ चुके हैं, तो साधारण भिन्नों को दशमलव में बदलना कठिन नहीं है। सामान्य भिन्नों को दशमलव में बदलने के लिए, यदि आप हाथ से गणना नहीं करना चाहते हैं, तो आप लंबे विभाजन, गुणा या कैलकुलेटर का भी उपयोग कर सकते हैं। एक बार जब आप विधि में महारत हासिल कर लेते हैं, तो आप भिन्नों को दशमलव में आसानी से बदलने में सक्षम होंगे।
कदम
विधि 1: 4 में से: लंबे विभाजन के साथ
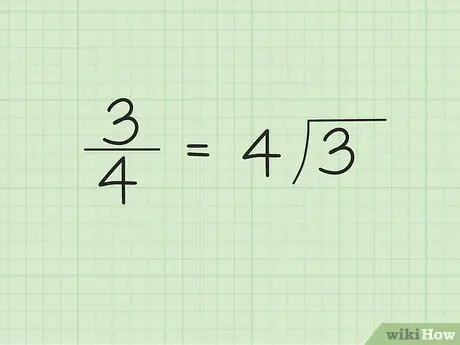
चरण 1. भाजक चिह्न के बाहर/बाईं ओर हर और भाजक चिह्न के अंदर/दाहिनी ओर अंश लिखें।
उदाहरण के लिए, मान लें कि हम 3/4 को दशमलव में बदलना चाहते हैं। भाजक चिह्न के बाहर/बाईं ओर “4” और भाजक चिह्न के अंदर/दाहिनी ओर “3” लिखें। "4" वह संख्या है जो विभाजित करती है और "3" वह संख्या है जो विभाजित होती है।

चरण 2. भाजक चिह्न के ऊपर "0", फिर एक दशमलव बिंदु (एक अल्पविराम) लिखें।
चूंकि यह एक भिन्न है जो मायने रखता है, परिणाम एक से कम होना चाहिए, इसलिए यह चरण बहुत महत्वपूर्ण है। उसके बाद, भाजक चिह्न के अंदर/दाहिनी ओर दशमलव चिह्न, फिर "0", संख्या "3" के बाद लिखें। भले ही "3" "3, 0" के बराबर हो, शून्य "3, 0" को "4" से विभाजित करने की अनुमति देता है।

चरण 3. लंबे विभाजन का उपयोग करके उत्तर की गणना करें।
लंबे विभाजन के साथ, अभी के लिए, दशमलव चिह्न को अनदेखा किया जा सकता है, इसलिए आपको केवल 30 को 4 से विभाजित करने की आवश्यकता है। यहां बताया गया है:
- सबसे पहले, 3, 0, जो 30 के रूप में गिना जाता है, को 4 से विभाजित करें। 4 से 30 के लिए निकटतम 4 x 7 = 28 है, 2 को छोड़कर। इसलिए, भाजक के ऊपर "0" के बाद "7", और "28" के नीचे "28" लिखें। 3, 0” भाजक चिह्न के अंदर/दाहिनी ओर। 28 के तहत, "2" लिखें, शेष 30 माइनस 28।
- इसके बाद, "3, 0" के बाद "0" लिखें ताकि यह "3, 00" हो जाए, जिसे भाजक प्रतीक के अंदर / दाईं ओर "300" माना जा सकता है। इस प्रकार, 0 को "2" के दाईं ओर कम किया जा सकता है ताकि "20" "4" से विभाज्य हो।
- "20" को "4" से विभाजित करने पर "5" के बराबर होता है। अतः भाजक चिन्ह के ऊपर "0.7" के बाद "5" लिखें ताकि वह "0.75" हो जाए।

चरण 4. अंतिम उत्तर लिखें।
तो, "3" को "4" से विभाजित करने पर "0.75" के बराबर होता है। उत्तर लिखिए। ख़त्म होना।
विधि 2 का 4: दोहराए जाने वाले दशमलवों को उत्पन्न करने वाले अंश
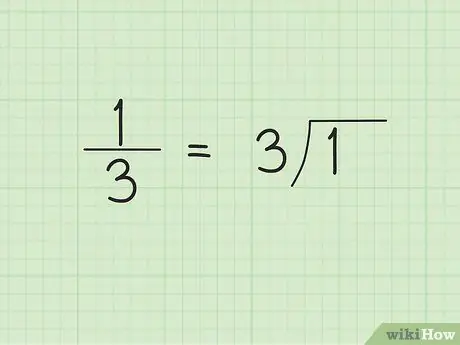
चरण 1. लंबा विभाजन विभाजन करें।
जब आप लंबे अंकों का विभाजन शुरू करते हैं, तो आप यह अनुमान लगाने में सक्षम नहीं हो सकते हैं कि परिणाम एक दोहराई जाने वाली दशमलव संख्या होगी। उदाहरण के लिए, मान लें कि हम सामान्य भिन्न 1/3 को दशमलव रूप में बदलना चाहते हैं। भाजक चिह्न के बाहर/बाईं ओर 3 या हर और भाजक चिह्न के अंदर/दाहिनी ओर 1 लिखें।

चरण 2. भाजक चिह्न के ऊपर एक 0, फिर एक दशमलव चिह्न लिखें।
चूंकि परिणाम 1 से कम होना चाहिए, यह चरण दशमलव रूप में लिखे जाने वाले उत्तर को तैयार करता है। दशमलव चिह्न भी संख्या "1" के दाईं ओर लिखा जाना चाहिए जो कि भाजक चिह्न के दाईं ओर स्थित है।
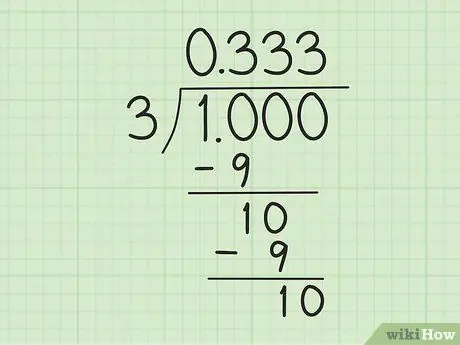
चरण 3. लांग डिवीजन डिवीजन की गणना शुरू करें।
"1" को "1, 0" से शुरू करें, जो "10" के रूप में गिना जाता है, ताकि यह "3" से विभाज्य हो। अगला, निम्न चरणों का पालन करें:
- 10 को 3 से भाग दें। 3 x 3 = 9 का उपयोग करके 1 का शेष प्राप्त करें। इसलिए भाजक चिह्न के ऊपर "0" के दाईं ओर 3 लिखें और शेष 1 प्राप्त करने के लिए 10 को 9 से घटाएं।
- एक और "10" प्राप्त करने के लिए नीचे "1" (पिछले चरण में शेष 10 घटा 9) के दाईं ओर एक "0" लिखें। जब फिर से "10" को "3" से विभाजित किया जाता है, तो वही प्रक्रिया दोहराई जाती है: भाजक चिह्न के ऊपर पहले "3" के दाईं ओर "3" लिखें और नए "10" को "9" से घटाएं।
- एक पैटर्न बनने तक जारी रखें। तुम्हें पता है कुछ अजीब है? यह विभाजन हमेशा के लिए चल सकता है। 10 हमेशा 3 से विभाज्य होता है: नीचे हमेशा एक "1" होगा और भाजक चिह्न के ऊपर दशमलव के बाद एक नया "3" होगा।
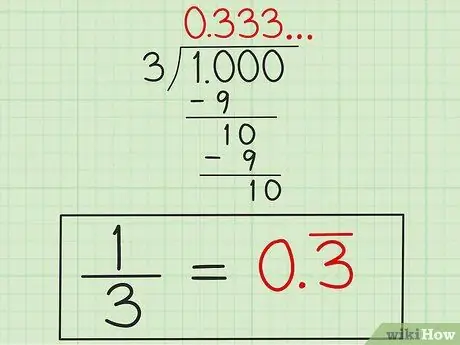
चरण 4. उत्तर लिखिए।
यह जानने के बाद कि "3" खुद को दोहराएगा, उत्तर "0, 3" के रूप में संख्या "3" (या "0, 33" दोनों संख्याओं "3" से ऊपर की रेखा के साथ एक पंक्ति के साथ) एक संकेत के रूप में लिखें कि संख्या "3" यह दोहराता रहता है। यह उत्तर दशमलव रूप 1/3 में है क्योंकि 1 को 3 से विभाजित करने पर अपने आप समाप्त नहीं होगा।
ऐसे कई अंश हैं जो दोहराए जाने वाले दशमलव उत्पन्न करते हैं, जैसे कि 2/9 ("0, 2" "2" दोहराव के साथ), 5/6 ("0, 83" "3" दोहराव के साथ), या 7/9 ("0, 7" के साथ "7" दोहराता रहता है)। यह पैटर्न हमेशा तब होता है जब हर 3 का गुणज होता है और अंश हर से विभाज्य नहीं हो सकता।
विधि 3 का 4: गुणा करके

चरण १. वह संख्या ज्ञात कीजिए जिसे भिन्न के हर से गुणा करके १०, १००, १,००० या आधार १० प्राप्त की जा सकती है।
यह लंबे विभाजन या कैलकुलेटर का उपयोग किए बिना अंशों को दशमलव में बदलने का एक आसान तरीका हो सकता है। सबसे पहले, केवल एक संख्या ज्ञात करें जिसे भिन्न के हर से गुणा करके 10, 100, 1,000, इत्यादि प्राप्त किया जा सकता है। ऐसा करने के लिए, पहले १०, फिर १००, फिर १,०००, और इसी तरह हर से विभाजित करें जब तक कि आपको एक पूर्णांक न मिल जाए। उदाहरण:
- 3/5. 10/5 = 2.2 एक पूर्णांक है। 2 को 5 से गुणा करके 10 बनाया जा सकता है। तो, 2 का उपयोग किया जा सकता है।
- 3/4. 10/4 = 2, 5. 2, 5 एक पूर्णांक नहीं है। 100/4 = 25. 25 एक पूर्णांक है। 25 को 4 से गुणा करके 100 बनाया जा सकता है। तो 25 का उपयोग किया जा सकता है।
- 5/16. 10/16 = 0, 625, 100/16 = 6, 25, 1,000/16 = 62, 5, 10,000/16 = 625। 625 प्राप्त पहला पूर्णांक है। 10,000 प्राप्त करने के लिए 625 को 16 से गुणा किया जा सकता है। तो, 625 का उपयोग किया जा सकता है।
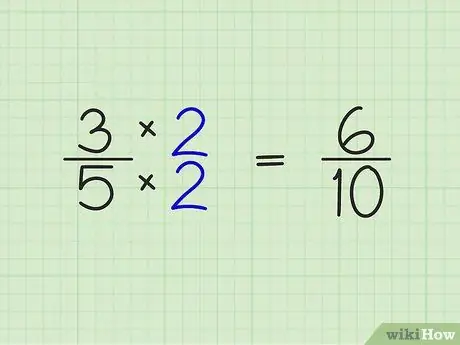
चरण 2. भिन्न के अंश और हर को पिछले चरण से प्राप्त पूर्ण संख्या से गुणा करें।
यह स्टेप काफी आसान है। पिछले चरण में आपको मिली पूर्ण संख्या से बस भिन्न के ऊपर और नीचे की संख्याओं को गुणा करें। उदाहरण:
- 3/5 x 2/2 = 6/10
- 3/4 x 25/25 = 75/100
- 5/16 x 625/625 = 3.125/10000

चरण 3. अंतिम उत्तर लिखें।
इसका उत्तर यह है कि हर में 0 की संख्या के अनुसार अंश को दशमलव से अंकित किया जाता है। बस गिनें कि हर में कितने 0 हैं। यदि हर में केवल 1 0 है, तो दशमलव बिंदु को 1 अंक से बाईं ओर ले जाएँ, और इसी तरह आगे भी। उदाहरण:
- 3/5 = 6/10 = 0, 6
- 3/4 = 75/100 = 0, 75
- 5/16 = 3.125/10.000 = 0, 3125
विधि 4 का 4: कैलकुलेटर के साथ

चरण 1. अंश को हर से विभाजित करें।
यह तरीका बहुत आसान है। अंश, अंश के शीर्ष पर संख्या, हर द्वारा, अंश के नीचे की संख्या को विभाजित करने के लिए बस एक कैलकुलेटर का उपयोग करें। उदाहरण के लिए, मान लें कि आप 3/4 को दशमलव में बदलना चाहते हैं। बस "3" दबाएं, फिर विभाजन चिह्न ("÷'"), फिर "4", और अंत में बराबर प्रतीक ("=")।

चरण 2. आपको मिलने वाले उत्तरों को लिख लें।
उत्तर 0.75 है। अतः, सामान्य भिन्न 3/4 का दशमलव रूप 0.75 है।
टिप्स
- यह जांचने के लिए कि आपका उत्तर सही है, भिन्न के हर से उत्तर को गुणा करें। यदि आपका उत्तर सही है, तो गुणन का गुणनफल भिन्न का अंश होता है।
- कुछ भिन्नों को तुलनीय भिन्न बनाकर दशमलव में परिवर्तित किया जा सकता है जिनके हर आधार १० (10, १००, १,०००, और इसी तरह) हैं। इसके बाद, दशमलव के सही रूप को लिखने के लिए स्थानीय मानों का उपयोग करें।







