किसी भिन्न को भिन्न से विभाजित करना पहली बार में भ्रमित करने वाला लग सकता है, लेकिन वास्तव में यह वास्तव में आसान है। आपको बस इतना करना है कि पलटें, गुणा करें और सरल करें! यह लेख आपको प्रक्रिया के बारे में बताएगा और आपको दिखाएगा कि भिन्न से भिन्न को विभाजित करना कितना आसान है।
कदम
2 का भाग 1: यह समझना कि भिन्नों को भिन्नों से कैसे विभाजित किया जाए
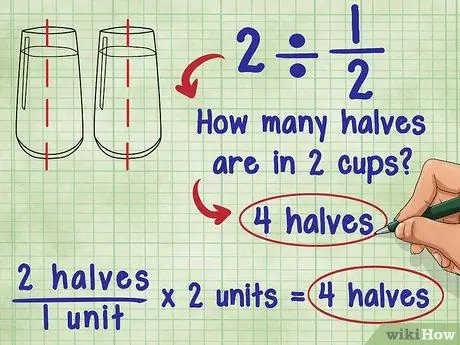
चरण 1. सोचें कि भिन्न से भाग देने का क्या अर्थ है।
के बारे में 2 ÷ 1/2 अदा से पूछा: "2 में कितने आधे होते हैं?" उत्तर 4 है क्योंकि प्रत्येक इकाई (1) में दो "आधे" होते हैं, और कुल 2 इकाइयाँ होती हैं: 2 "आधा" / 1 इकाई * 2 इकाइयाँ = 4 "आधा"।
- एक गिलास पानी का उपयोग करके समान समीकरण की कल्पना करने का प्रयास करें: 2 गिलास पानी में कितने और आधा गिलास पानी है? आप प्रत्येक गिलास पानी में ढाई कप पानी डाल सकते हैं। इसका मतलब है, मूल रूप से, आप "आधा" गिलास पानी जोड़ते हैं, और आपके पास दो गिलास हैं: 2 "आधा" / 1 कप * 2 कप = 4 "आधा"।
- इसका मतलब यह है कि यदि आप जिस भिन्न को विभाजित कर रहे हैं वह 0 और 1 के बीच है, तो उत्तर हमेशा मूल संख्या से बड़ा होता है! यह तब सत्य होता है जब आप किसी पूर्ण संख्या या भिन्न को भिन्न से भाग देते हैं।

चरण 2. समझें कि विभाजित करना गुणा के विपरीत है।
इस प्रकार, भिन्न से भाग देने पर भिन्न के व्युत्क्रम से गुणा करके हल किया जा सकता है। एक भिन्न का व्युत्क्रम (जिसे "गुणा व्युत्क्रम" भी कहा जाता है) वह भिन्न होता है जो उल्टा होता है, जिससे अंश और हर की अदला-बदली होती है। एक क्षण में, हम भिन्नों को भिन्नों से विभाजित करेंगे, दूसरी भिन्न का व्युत्क्रम ज्ञात करके और दोनों भिन्नों को गुणा करके। हालाँकि, आइए पहले कुछ विरोधों को देखें:
- 3/4 का व्युत्क्रम 4/3 है।
- 7/5 का विपरीत 5/7 है।
- 1/2 का व्युत्क्रम 2/1 या 2 है।
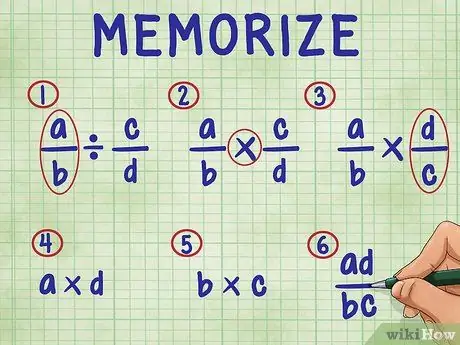
चरण 3. एक भिन्न को भिन्न से भाग देने के लिए निम्नलिखित चरणों को याद रखें।
क्रम में, चरणों में शामिल हैं:
- समीकरण में बस पहले अंश को छोड़ दें।
- भाग चिह्न को गुणन चिह्न में बदलें।
- दूसरी भिन्न को उल्टा करें (इसका व्युत्क्रम ज्ञात कीजिए)।
- दोनों भिन्नों के अंश (शीर्ष संख्या) को गुणा करें। गुणन परिणाम आपके उत्तर का अंश (शीर्ष) है।
- दोनों भिन्नों के हर (निचली संख्या) को गुणा करें। उत्पाद का उत्पाद आपके उत्तर का हर है।
- अपने भिन्नों को उनके सरलतम शब्दों में सरल बनाकर सरल करें।
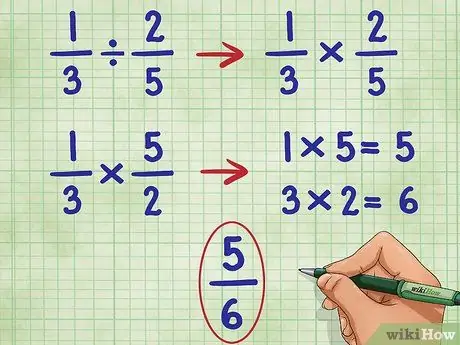
चरण ४. १/३ २/५ उदाहरण के लिए इन चरणों का पालन करें।
हम पहले भिन्न को छोड़कर, और भाग चिह्न को गुणन चिह्न में परिवर्तित करके प्रारंभ करेंगे:
- 1/3 ÷ 2/5 = बन जाता है:
- 1/3 * _ =
- अब, हम दूसरी भिन्न (2/5) को उल्टा करके उसका व्युत्क्रम ज्ञात करते हैं, जो कि 5/2 है:
- 1/3 * 5/2 =
- अब, दोनों भिन्नों के अंश (शीर्ष संख्या) को 1*5 = 5 से गुणा करें।
- 1/3 * 5/2 = 5/
- अब, दोनों भिन्नों के हर (निचली संख्या) को 3*2 = 6 से गुणा करें।
- अब हमारे पास है: 1/3 * 5/2 = 5/6
- इस भिन्न को और सरल नहीं किया जा सकता है, इसलिए हमारे पास हमारा उत्तर है।

चरण 5. आपको याद रखने में मदद करने के लिए निम्नलिखित तुकबंदी याद करने का प्रयास करें:
"अंशों को विभाजित करना आसान है, दूसरे अंश को उलट दें, फिर गुणा करें। खाने का समय होने से पहले इसे सरल बनाना न भूलें।"
एक अन्य सहायक अनुस्मारक सहायता आपको बताती है कि समीकरण के प्रत्येक भाग के साथ क्या करना है: "मुझे (पहला अंश), मुझे बदलें (विभाजन चिह्न), मुझे उल्टा करें (दूसरा अंश)।
2 का भाग 2: समस्याओं में भिन्नों द्वारा भिन्नों को विभाजित करना
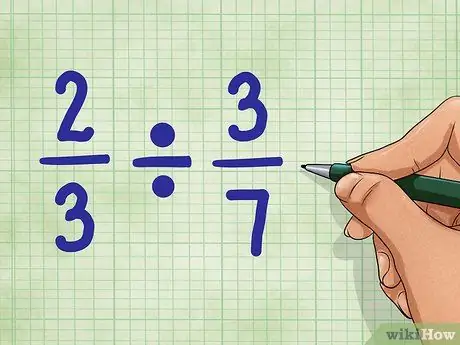
चरण 1. नमूना प्रश्नों से शुरू करें।
आइए उपयोग करें 2/3 ÷ 3/7. यह प्रश्न 3/7 के बराबर भागों की संख्या पूछता है, जो मान 2/3 में पाया जा सकता है। चिंता मत करो। यह उतना मुश्किल नहीं है जितना लगता है!
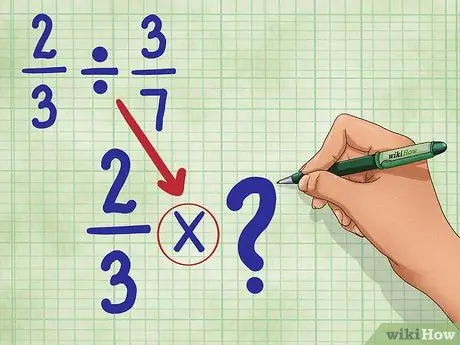
चरण 2. भाग चिह्न को गुणन चिह्न में बदलें।
आपका नया समीकरण होगा: 2/3 * _ (हम इसे एक पल में खाली कर देंगे।)
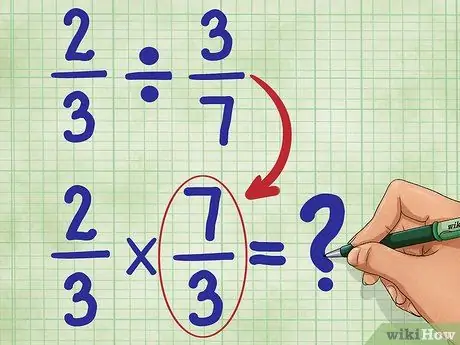
चरण 3. अब दूसरी भिन्न का व्युत्क्रम ज्ञात कीजिए।
इसका मतलब है कि 3/7 फ़्लिप करना ताकि अंश (3) अब सबसे नीचे हो, और हर (7) अब सबसे ऊपर हो। 3/7 का व्युत्क्रम 7/3 है। अब, अपना नया समीकरण लिखें:
2/3 * 7/3 = _

चरण 4. अपने भिन्नों को गुणा करें।
सबसे पहले, दोनों भिन्नों के अंशों को गुणा करें: 2 * 7 = 14. 14 आपके उत्तर का अंश (शीर्ष संख्या) है। फिर, दोनों भिन्नों के हरों को गुणा करें: 3 * 3 = 9. 9 आपके उत्तर का हर (निचला संख्या) है। अब, आप जानते हैं कि 2/3 * 7/3 = 14/9.
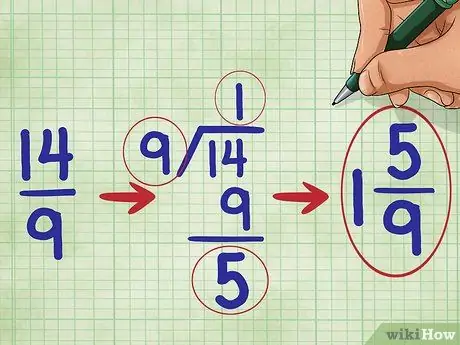
चरण 5. अपने भिन्न को सरल कीजिए।
इस समस्या में, क्योंकि भिन्न का अंश हर से बड़ा होता है, हम जानते हैं कि हमारी भिन्न 1 से बड़ी है। हमें इसे मिश्रित संख्या में बदलना होगा। (एक मिश्रित संख्या एक पूर्ण संख्या है और एक अंश संयुक्त है, उदाहरण के लिए 1 2/3।))
-
सबसे पहले, अंश को विभाजित करें
चरण 14. साथ 9.
संख्या १४ को ९ से विभाजित करने पर, ५ के शेष के साथ एक के बराबर होती है, इसलिए आपको अपना सरलीकृत अंश इस प्रकार लिखना चाहिए: 1 5/9 ("एक पांच-नौवां")।
- रुको, तुम्हें जवाब मिल गया है! आप निर्दिष्ट कर सकते हैं कि अब आप भिन्न को सरल नहीं कर सकते क्योंकि हर अंश से विभाज्य नहीं है (9, 5 से विभाज्य नहीं है) और अंश एक अभाज्य संख्या है, या एक पूर्णांक है जो केवल एक और स्वयं संख्या से विभाज्य है।
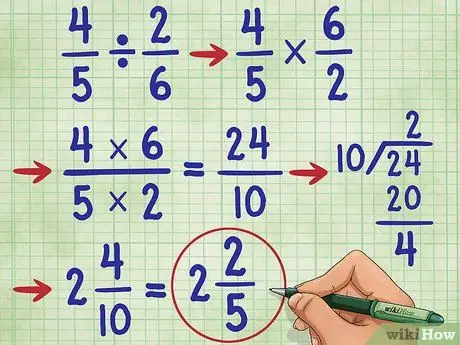
चरण 6. एक और उदाहरण आज़माएं
आइए प्रश्न का प्रयास करें 4/5 ÷ 2/6 =. सबसे पहले, विभाजन चिह्न को गुणन चिह्न में बदलें (4/5 * _ =), तो 2/6 का व्युत्क्रम ज्ञात कीजिए, जो कि 6/2 है। अब, आपके पास समीकरण है: 4/5 * 6/2 =_. अब, अंश को गुणा करें, 4 * 6 = 24, और भाजक 5* 2 = 10. अब आपके पास है 4/5 * 6/2 = 24/10.
अब भिन्न को सरल कीजिए। चूंकि अंश हर से बड़ा है, इसलिए हमें इस भिन्न को मिश्रित संख्या में बदलना होगा।
- सबसे पहले, अंश को हर से विभाजित करें, (२४/१० = २ शेष ४).
- उत्तर इस प्रकार लिखें 2 4/10. हम अब भी इस भिन्न को फिर से सरल बना सकते हैं!
- ध्यान दें कि 4 और 10 सम संख्याएं हैं। तो, इसे सरल बनाने के लिए पहला कदम प्रत्येक संख्या को 2 से विभाजित करना है। हमें 2/5 मिलता है।
- चूँकि हर (5) अंश (2) से विभाज्य नहीं है और 5 एक अभाज्य संख्या है, हम जानते हैं कि इस भिन्न को और सरल नहीं किया जा सकता है। तो, हमारा जवाब है: 2 2/5.

चरण 7. भिन्नों को सरल बनाने में अतिरिक्त सहायता प्राप्त करें।
आपने भिन्नों को एक-दूसरे से विभाजित करने का प्रयास करने से पहले शायद यह सीखने में बहुत समय बिताया हो कि भिन्नों को सरल कैसे बनाया जाए। हालाँकि, यदि आपको एक पुनश्चर्या या किसी अन्य सहायता की आवश्यकता है, तो कुछ बेहतरीन ऑनलाइन लेख हैं जो आपकी बहुत मदद कर सकते हैं।
संबंधित विकिहाउ लेख
- सामान्य भिन्नों को दशमलव में बदलना
- एक वृत्त के क्षेत्रफल की गणना
- सिंथेटिक डिवीजन का उपयोग करके बहुपदों को विभाजित करना
- मिश्रित भिन्नों को विभाजित करना







