हर कोई गणित सीख सकता है चाहे वे पहले से ही स्कूल में उच्च स्तर पर हों या जो मूल बातें फिर से सुधारना चाहते हों। गणित में एक अच्छा शिक्षार्थी कैसे बनें, इस पर चर्चा करने के बाद, यह लेख आपको गणित की बुनियादी प्रगति सिखाएगा और आपको प्रत्येक अभ्यास में सीखने के लिए आवश्यक बुनियादी तत्व प्रदान करेगा। फिर, यह लेख अंकगणित सीखने की मूल बातें पर चर्चा करेगा, जो प्राथमिक विद्यालय के बच्चों और विज्ञान के इस क्षेत्र की मूल बातें सीखने के इच्छुक सभी लोगों की मदद करेगा।
कदम
६ का भाग १: एक अच्छा गणित छात्र बनने की कुंजी

चरण 1. कक्षा में उपस्थित हों।
जब आप कक्षा को याद करते हैं, तो आपको सहपाठियों से या अपनी पाठ्यपुस्तक से अवधारणाओं को सीखना चाहिए। आपको किसी मित्र से उतना पाठ सारांश कभी नहीं मिलेगा जितना आपको अपने शिक्षक से मिलता है।
- समय पर कक्षा में आना। इसके बजाय, थोड़ा जल्दी पहुंचें और अपनी नोटबुक को सही जगह पर खोलें, अपनी पाठ्यपुस्तक खोलें और अपना कैलकुलेटर निकाल लें ताकि जब आपका शिक्षक पढ़ाने के लिए तैयार हो तो आप शुरू करने के लिए तैयार हों।
- अगर आप बीमार हैं तो ही ट्रूट करें। यदि आप वास्तव में कक्षा से चूक जाते हैं, तो अपने सहपाठियों से यह पता लगाने के लिए कहें कि शिक्षक किस बारे में बात कर रहा था और उसे क्या गृहकार्य दिया गया था।

चरण 2. अपने शिक्षक के साथ काम करें।
यदि आपका शिक्षक कक्षा के सामने किसी समस्या पर काम कर रहा है, तो अपनी नोटबुक में समस्या पर काम करके शिक्षक के साथ काम करें।
- सुनिश्चित करें कि आपके नोट्स स्पष्ट और पढ़ने में आसान हैं। केवल प्रश्न न लिखें। शिक्षक द्वारा कही गई किसी भी बात को भी लिख लें, जो समझाई जा रही अवधारणाओं के बारे में आपकी समझ में सुधार कर सके।
- अपने शिक्षक द्वारा दिए गए नमूना प्रश्नों को पूरा करें। जब आप काम करते हैं तो शिक्षक कक्षा में घूमता है, पूछे गए प्रश्नों के उत्तर दें।
- जब शिक्षक किसी समस्या का समाधान करे तो भाग लें। शिक्षक द्वारा आपको बुलाए जाने की प्रतीक्षा न करें। जब आप उत्तर जानते हैं तो उत्तर देने की पेशकश करें, और यदि आप सिखाई जा रही सामग्री के बारे में अनिश्चित हैं तो प्रश्न पूछने के लिए अपना हाथ उठाएं।

चरण 3. अपना गृहकार्य उसी दिन करें जिस दिन आपका गृहकार्य दिया जाता है।
यदि आप उसी दिन अपना गृहकार्य करते हैं, तो यह अवधारणा आपके दिमाग में अभी भी ताजा है। कभी-कभी, एक ही दिन में अपना गृहकार्य पूरा करना संभव नहीं होता है। सुनिश्चित करें कि आपका होमवर्क कक्षा में जाने से पहले हो गया है।

चरण 4. यदि आपको सहायता की आवश्यकता हो तो कक्षा के बाहर कार्य करें।
अवकाश के दौरान या कार्यालय समय के दौरान अपने शिक्षक से मिलें।
- यदि आपके विद्यालय में एक गणित केंद्र है, तो उसके खुलने का समय पता करें और मदद मांगें।
- एक अध्ययन समूह में शामिल हों। एक अच्छे अध्ययन समूह में आम तौर पर विभिन्न स्तरों की क्षमता वाले 4 या 5 लोग होते हैं। यदि आप गणित में "सी" छात्र हैं, तो "ए" या "बी" ग्रेड वाले 2 या 3 छात्रों के समूह में शामिल हों ताकि आप अपने कौशल में सुधार कर सकें। उन छात्रों के समूह में शामिल होने से बचें, जिनके ग्रेड आपके से कम हैं।
6 का भाग 2: स्कूल में गणित सीखना

चरण 1. अंकगणित से शुरू करें।
अधिकांश विद्यालयों में छात्र प्राथमिक विद्यालय में अंकगणित सीखते हैं। अंकगणित में जोड़, घटाव, गुणा और भाग की मूल बातें शामिल हैं।
- प्रश्नों का अभ्यास करें। मूल बातें सही ढंग से याद करने का सबसे अच्छा तरीका अंकगणितीय समस्याओं को बार-बार करना है। ऐसे सॉफ़्टवेयर की तलाश करें जो आपको काम करने के लिए विभिन्न प्रकार की गणित की विभिन्न समस्याएं दे सकें। साथ ही, अपनी गति को सुधारने के लिए समय-सीमा की समस्याओं को देखें।
- आप अंकगणितीय समस्याओं को ऑनलाइन भी ढूंढ सकते हैं, और आप अपने मोबाइल डिवाइस पर अंकगणितीय ऐप्स डाउनलोड कर सकते हैं।

चरण 2. पूर्व-बीजगणित के साथ जारी रखें।
यह अभ्यास आपको मूल तत्व प्रदान करेगा जिनकी आपको बाद में बीजगणित की समस्याओं को हल करने की आवश्यकता होगी।
- भिन्न और दशमलव के बारे में जानें। आप भिन्न और दशमलव को जोड़ना, घटाना, गुणा करना और भाग देना सीखेंगे। भिन्नों के संबंध में, आप भिन्नों को घटाना और संयुक्त संख्याओं का अनुवाद करना सीखेंगे। दशमलव के संबंध में, आप स्थानीय मानों को समझेंगे, और आप कहानी की समस्याओं में दशमलव का उपयोग करने में सक्षम होंगे।
- अनुपात, अनुपात और प्रतिशत के बारे में जानें। ये अवधारणाएँ आपको तुलना करना सीखने में मदद करेंगी।
- बुनियादी ज्यामिति से अपना परिचय दें। आप 3D आकार और अवधारणाएँ सीखेंगे। आप क्षेत्र, परिधि, आयतन और सतह क्षेत्र जैसी अवधारणाओं के साथ-साथ समानांतर और लंबवत रेखाओं और कोणों के बारे में जानकारी भी सीखेंगे।
- कुछ बुनियादी आंकड़ों को समझें। पूर्व-बीजगणित में, आँकड़ों से आपके परिचय में आम तौर पर ग्राफ़, स्कैटर चार्ट, स्टैम्प प्लॉट चार्ट और हिस्टोग्राम जैसे दृश्य शामिल होते हैं।
- बीजगणित की मूल बातें जानें। इसमें चर युक्त सरल समीकरणों को हल करना, वितरण गुण जैसे गुणों के बारे में सीखना, सरल समीकरण बनाना और असमानताओं को हल करना जैसी अवधारणाएँ शामिल हैं।
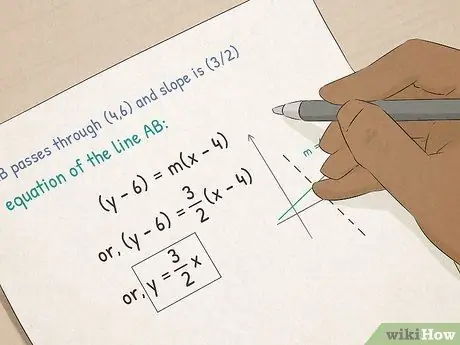
चरण 3. बीजगणित I के लिए अग्रिम।
बीजगणित के अपने पहले वर्ष में, आप बीजगणित में शामिल बुनियादी प्रतीकों के बारे में जानेंगे। आप यह भी सीखेंगे:
- चर वाले समीकरणों और असमानताओं को हल करें। आप सीखेंगे कि इन समस्याओं को कागज पर कैसे हल किया जाए और उन्हें चित्रों के साथ कैसे हल किया जाए।
- कहानी की समस्याओं को हल करें। आपको आश्चर्य होगा कि भविष्य में आपको कितनी रोज़मर्रा की समस्याओं का सामना करना पड़ेगा जिनके लिए बीजीय कहानी की समस्याओं को हल करने की क्षमता की आवश्यकता होती है। उदाहरण के लिए, आप अपने बैंक खाते या निवेश पर अर्जित ब्याज दर का पता लगाने के लिए बीजगणित का उपयोग करेंगे। आप अपनी कार की गति के आधार पर यह पता लगाने के लिए बीजगणित का उपयोग कर सकते हैं कि आपको कितनी देर तक यात्रा करनी चाहिए।
- प्रतिपादकों के साथ काम करें। जब आप बहुपद समीकरणों को हल करना शुरू करते हैं (ऐसे व्यंजक जिनमें संख्याएँ और चर होते हैं), तो आप समझेंगे कि घातांक का उपयोग कैसे किया जाता है। इसमें संभवतः वैज्ञानिक संकेतन वाले अभ्यास शामिल होंगे। एक बार जब आप घातांक में महारत हासिल कर लेते हैं, तो आप बहुपद व्यंजकों को जोड़ना, घटाना, गुणा और भाग करना सीख सकते हैं।
- वर्गमूल और वर्गमूल की समस्याओं को हल करें। जैसे-जैसे आप इस विषय में महारत हासिल करेंगे, आप कई संख्याओं के वर्गों को याद करने में सक्षम होंगे। आप उन समीकरणों के साथ भी काम करने में सक्षम होंगे जिनके वर्गमूल हैं।
- कार्यों और रेखांकन को समझें। बीजगणित में, आप ग्राफिक समीकरणों के बारे में जानेंगे। आप सीखेंगे कि किसी रेखा के ढलान की गणना कैसे करें, बिंदु-ढलान के रूप में समीकरण कैसे डालें, और ढलान-अवरोधन फॉर्म का उपयोग करके रेखा के x-और-y स्लाइस की गणना कैसे करें।
- समीकरणों की प्रणाली का पता लगाएं। कभी-कभी, आपको चर x और y के साथ 2 अलग-अलग समीकरण दिए जाते हैं, और आपको दोनों समीकरणों के लिए x या y के लिए हल करना होता है। सौभाग्य से, आप रेखांकन, प्रतिस्थापन और जोड़ सहित इन समीकरणों को हल करने के लिए बहुत सी तरकीबें सीखेंगे।

चरण 4. ज्यामिति का अध्ययन करें।
ज्यामिति में, आप रेखाओं, खंडों, कोणों और आकृतियों के गुणों के बारे में जानेंगे।
- आप कई प्रमेयों और उपफलों को याद करेंगे जो आपको ज्यामिति के नियमों को समझने में मदद करेंगे।
- आप सीखेंगे कि एक वृत्त के क्षेत्रफल की गणना कैसे करें, पाइथागोरस प्रमेय का उपयोग कैसे करें और एक विशेष त्रिभुज के कोणों और भुजाओं के बीच संबंध कैसे खोजें।
- आप भविष्य के मानकीकृत परीक्षणों जैसे SAT, ACT और GRE में ज्यामिति के कई प्रश्न देखेंगे।
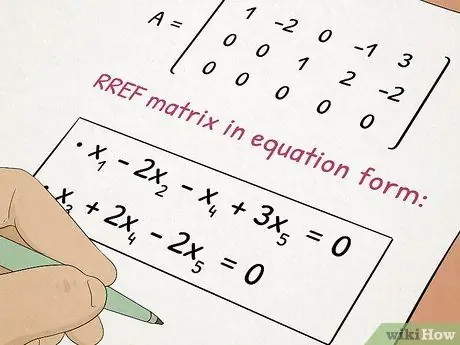
चरण 5. बीजगणित II कक्षा लें।
बीजगणित II द्विघात समीकरणों और मैट्रिक्स जैसे जटिल विषयों को जोड़ते हुए आपके द्वारा बीजगणित I में सीखी गई अवधारणाओं पर आधारित है।
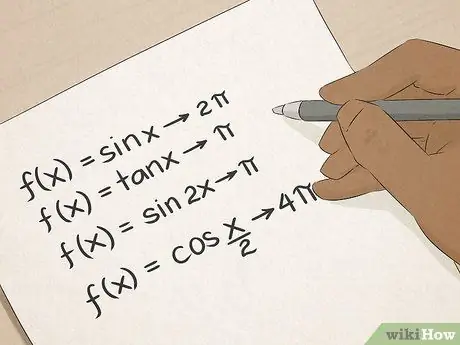
चरण 6. मास्टर त्रिकोणमिति।
आप त्रिकोणमितीय शब्दों को जानते हैं: साइन, कोसाइन, स्पर्शरेखा, और इसी तरह। त्रिकोणमिति आपको कोणों और रेखा की लंबाई की गणना करने के कई व्यावहारिक तरीके सिखाएगी, और ये कौशल निर्माण, वास्तुकला, इंजीनियरिंग या सर्वेक्षण में काम करने वाले लोगों के लिए अमूल्य होंगे।
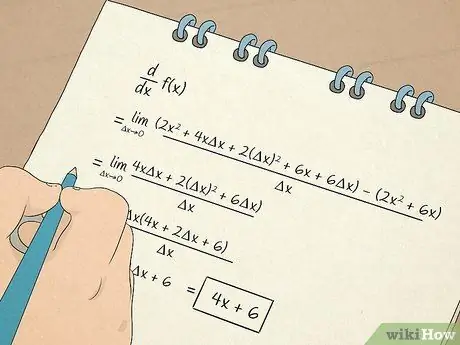
चरण 7. कलन गणना करें।
कैलकुलस डराने वाला लग सकता है, लेकिन यह संख्याओं के व्यवहार या आपके आसपास की दुनिया को समझने के लिए एक अद्भुत उपकरण है।
- कैलकुलस आपको कार्य और सीमाएं सिखाएगा। आप ई ^ एक्स और लॉगरिदमिक कार्यों सहित उपयोगी कार्यों की संख्या व्यवहार देखेंगे।
- आप यह भी सीखेंगे कि डेरिवेटिव के साथ गणना और काम कैसे करें। पहला अवकलज आपको समीकरण की स्पर्शरेखा रेखा के ढलान के आधार पर जानकारी देता है। उदाहरण के लिए, एक व्युत्पन्न आपको वह दर बताता है जिस पर एक गैर-रैखिक स्थिति में कुछ बदलता है। दूसरा व्युत्पन्न आपको बताएगा कि क्या फ़ंक्शन एक निश्चित अंतराल पर बढ़ता है या घटता है ताकि आप किसी फ़ंक्शन की अंतराल को निर्धारित कर सकें।
- इंटीग्रल आपको सिखाएंगे कि एक वक्र के साथ-साथ उसके आयतन के क्षेत्र की गणना कैसे करें।
- हाई स्कूल में कैलकुलस आमतौर पर अनुक्रमों और अनुक्रमों में समाप्त होता है। हालांकि छात्रों को सर्किट के लिए कई आवेदन नहीं दिखाई देंगे, अंतर समीकरणों का अध्ययन करने वालों के लिए सर्किट महत्वपूर्ण हैं।
६ का भाग ३: गणित की बुनियादी बातें--मास्टर जोड़

चरण 1. "+1" तथ्यों से शुरू करें।
किसी संख्या में 1 जोड़ने पर आप संख्या रेखा पर सबसे बड़ी संख्या पर पहुंच जाते हैं। उदाहरण के लिए, 2 + 1 = 3।
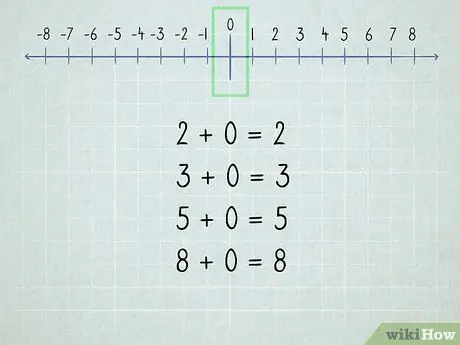
चरण 2. शून्य को समझें।
शून्य में जोड़ी गई सभी संख्याएँ समान संख्याएँ हैं क्योंकि "शून्य" का अर्थ है "कोई नहीं।"

चरण 3. डबल नंबर सीखें।
एकाधिक संख्याएँ एक समस्या है जिसमें दो समान संख्याओं को जोड़ना शामिल है। उदाहरण के लिए, 3 + 3 = 6 एक समीकरण का एक उदाहरण है जिसमें कई संख्याएँ शामिल हैं।

चरण 4. अन्य अतिरिक्त समाधानों के बारे में जानने के लिए मानचित्रण का उपयोग करें।
नीचे दिए गए उदाहरण में, आप मैप करके सीखते हैं कि जब आप 3 से 5, 2 और 1 जोड़ते हैं तो क्या होता है। "2 से जोड़ें" समस्या को स्वयं आज़माएं।

चरण 5. तब तक जारी रखें जब तक संख्या 10 से अधिक न हो जाए।
10 से बड़ी संख्या प्राप्त करने के लिए 3 संख्याओं को एक साथ जोड़ना सीखें।
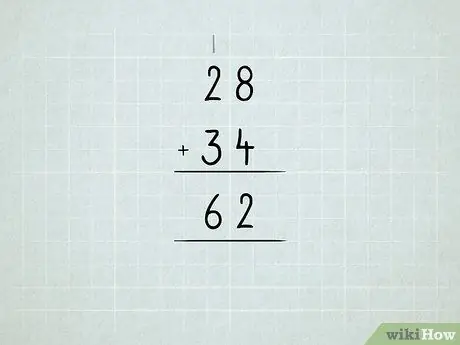
चरण 6. बड़ी संख्याएँ जोड़ें।
इकाइयों को दहाई, दहाई से सैकड़ों, इत्यादि में पुनर्समूहित करने के बारे में जानें।
- पहले सही कॉलम में संख्याओं को जोड़ें। 8 + 4 = 12, जिसका मतलब है कि आपके पास 1 नंबर 10 और 2 नंबर 1 है। यूनिट कॉलम के तहत नंबर 2 लिखें।
-
दहाई के कॉलम में नंबर 1 लिखिए।
-
दहाई के कॉलम को पूरी तरह से जोड़ दें।
भाग ४ का ६: गणितीय बुनियादी सिद्धांत--कमी रणनीतियाँ

चरण 1. "पिछड़े 1 अंक" से शुरू करें।
किसी संख्या में से 1 घटाने पर आपको 1 अंक वापस मिल जाता है। उदाहरण के लिए, 4 - 1 = 3।

चरण 2. डबल नंबर घटाना सीखें।
उदाहरण के लिए, आप संख्या ५ + ५ को जोड़कर १० प्राप्त करते हैं। १० - ५ = ५ प्राप्त करने के लिए बस समीकरण को पीछे की ओर लिखें।
- यदि ५ + ५ = १०, तो १० - ५ = ५।
-
यदि 2 + 2 = 4, तो 4 - 2 = 2।

चरण 3. तथ्य परिवार को याद करें।
उदाहरण के तौर पे:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

चरण 4. लुप्त संख्याएँ ज्ञात कीजिए।
उदाहरण के लिए, _ + 1 = 6 (उत्तर 5 है)।

चरण 5. घटाव के तथ्य को 20 तक याद रखें।

चरण 6. बिना उधार लिए 2-अंकीय संख्याओं में से 1-अंकीय संख्याओं को घटाने का अभ्यास करें।
इकाई के कॉलम में संख्याओं को घटाएं और दहाई के कॉलम में संख्याओं को घटाएं।
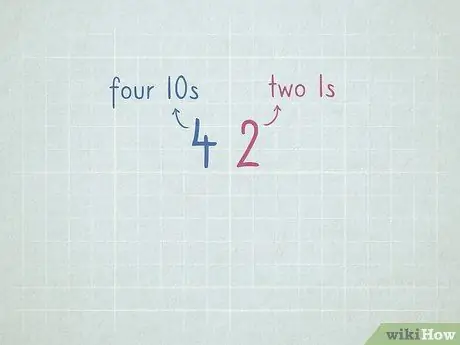
चरण 7. उधार लेकर घटाने की तैयारी के लिए स्थानीय मान का अभ्यास करें।
- 32 = 3 नंबर 10 और 2 नंबर 1.
- ६४ = ६ संख्याएँ १० और ४ संख्याएँ १।
- 96 = _ संख्या 10 और _ संख्या 1।
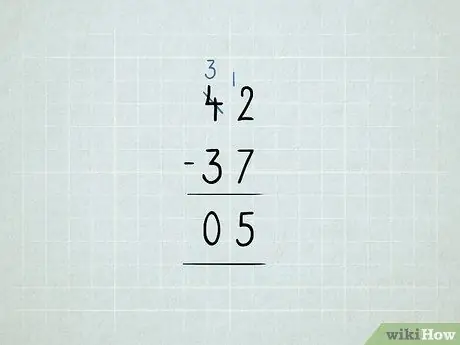
चरण 8. उधार लेकर घटाएं।
- आप 42 - 37 घटाना चाहते हैं। आप इकाइयों के कॉलम में 2 - 7 घटाने की कोशिश करके शुरू करते हैं। पता चला, यह काम नहीं किया!
-
दहाई के कॉलम से 10 की संख्या उधार लें और इसे इकाई के कॉलम में रखें। अब आपके पास 4 10 के बजाय 3 10 हैं। अब आपके पास 2 1 के बजाय 12 1 हैं।
-
पहले अपने यूनिट कॉलम को घटाएं: 12 - 7 = 5। फिर, दहाई कॉलम की जांच करें। चूँकि ३ - ३ = ०, आपको संख्या ० लिखने की आवश्यकता नहीं है। आपका उत्तर ५ है।
भाग ५ का ६: गणित की बुनियादी बातें--मास्टर गुणन

चरण 1. संख्या 1 और संख्या 0 से प्रारंभ करें।
वे सभी संख्याएँ जिन्हें 1 से गुणा किया जाता है, वे सभी संख्याएँ स्वयं संख्या के समान होती हैं। किसी भी संख्या को 0 से गुणा करने पर शून्य होता है।

चरण 2. गुणन तालिका को याद करें।

चरण 3. एकल अंक गुणन समस्याओं के साथ अभ्यास करें।

चरण 4. 2-अंकीय संख्या को 1-अंकीय संख्या से गुणा करें।
- नीचे दाईं संख्या को ऊपर दाईं ओर से गुणा करें।
-
निचले दाएं नंबर को ऊपर बाएं नंबर से गुणा करें।
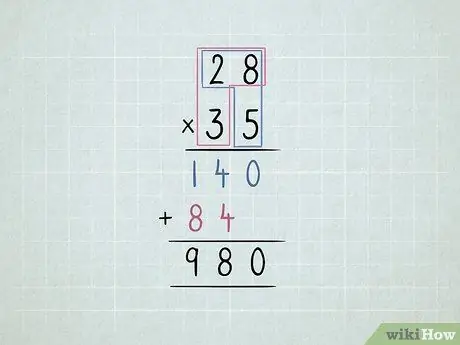
चरण 5. 2 2-अंकीय संख्याओं को गुणा करें।
- निचले दाएं नंबर को ऊपर दाएं नंबर से और फिर ऊपर बाएं नंबर से गुणा करें।
-
दूसरी पंक्ति को एक अंक बाईं ओर ले जाएँ।
- नीचे बाईं ओर की संख्या को ऊपर दाईं ओर और फिर ऊपर बाईं ओर की संख्या से गुणा करें।
-
सभी कॉलम जोड़ें।
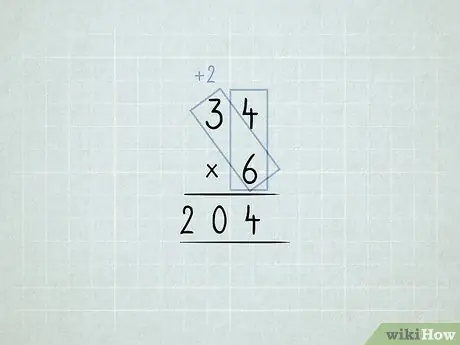
चरण 6. स्तंभों को गुणा और पुनर्समूहित करें।
- आप 34 x 6 गुणा करना चाहते हैं। आप इकाइयों के कॉलम (4 x 6) को गुणा करके शुरू करते हैं, लेकिन आपके पास इकाई के कॉलम में 24 1 नहीं हो सकते।
-
यूनिट कॉलम में 4 1s स्टोर करें। 2 10s को दहाई के कॉलम में ले जाएँ।
-
6 x 3 गुणा करें, जो 18 के बराबर है। आपके द्वारा स्थानांतरित किए गए 2 को जोड़ें, जो 20 के बराबर है।
भाग ६ का ६: गणितीय बुनियादी सिद्धांत--विभाजन की समस्याएं प्रकट करें

चरण 1. गुणन के विपरीत विभाजन के बारे में सोचें।
#* यदि ४ x ४ = १६, तो १६ / ४ = ४।
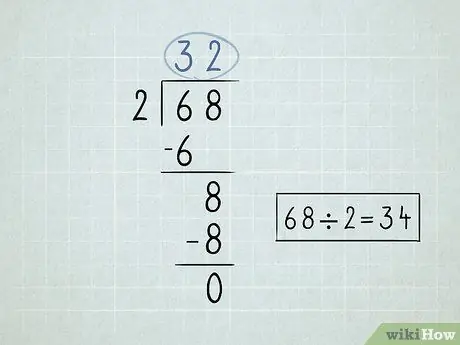
चरण 2. अपनी विभाजन समस्या लिखिए।
- भाजक चिह्न के नीचे पहली संख्या से विभाजन चिह्न, या भाजक के बाईं ओर की संख्या को विभाजित करें। चूँकि 6/2 = 3, आप संख्या 3 को भाग चिन्ह के ऊपर लिखेंगे।
-
भाज्य चिह्न के ऊपर की संख्या को भाजक से गुणा करें। परिणाम को भाग चिन्ह के तहत पहली संख्या के नीचे ले आओ। चूँकि 3 x 2 = 6, तो आप संख्या 6 को नीचे कर देंगे।
- आपके द्वारा लिखे गए 2 नंबरों को घटाएं। ६ - ६ = ०. आप ० को खाली छोड़ सकते हैं, क्योंकि आप आमतौर पर ० से संख्याएँ शुरू नहीं करते हैं।
-
दूसरी संख्या को नीचे लाएँ जो भाग चिन्ह के नीचे है।
- उस संख्या को विभाजित करें जिसे आप भाजक से नीचे लाते हैं। इस स्थिति में, 8/2 = 4. संख्या 4 को भाग चिह्न के ऊपर लिखिए।
-
भाजक से ऊपरी दाएँ संख्या को गुणा करें और संख्या को नीचे लाएँ। 4 x 2 = 8.
-
उन नंबरों को घटाएं। अंतिम घटाव शून्य लौटाता है, जिसका अर्थ है कि आपने समस्या हल कर ली है। ६८ x २ = ३४.

चरण 3. शेषफल की भी गणना कीजिए।
कुछ भाजक पूरी तरह से अन्य संख्याओं में विभाजित नहीं हैं। यदि आपने अंतिम घटाव पूरा कर लिया है, और आपके पास प्राप्त करने के लिए कोई और संख्या नहीं है, तो अंतिम संख्या शेष है।







