क्या आप नहीं जानते कि कैलकुलेटर का उपयोग किए बिना रैखिक समीकरण कैसे बनाएं? सौभाग्य से, रैखिक समीकरणों को रेखांकन करना काफी आसान है यदि आप जानते हैं कि कैसे। आपको बस अपने समीकरण के बारे में कुछ बातें समझनी हैं और आप इसे करने में सक्षम होंगे। चलो शुरू करो।
कदम
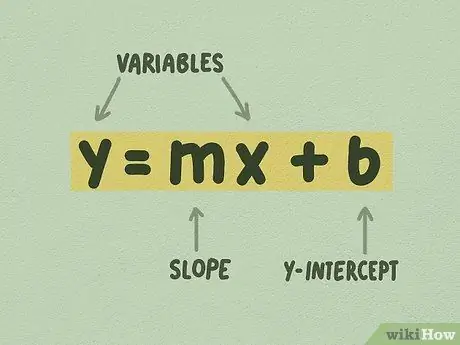
चरण 1. सुनिश्चित करें कि रैखिक समीकरण का रूप y = mx + b है।
इस आकृति को y-अवरोधन रूप कहा जाता है, और संभवतः रैखिक समीकरणों को रेखांकन करने के लिए उपयोग करने का सबसे आसान रूप है। समीकरण में मान का पूर्णांक होना आवश्यक नहीं है। अक्सर, आप एक ऐसा समीकरण देखेंगे जो इस तरह दिखता है: y = 1/4x + 5, जहाँ 1/4 m है और 5 b है।
- मी को "ढलान" या कभी-कभी "ढाल" कहा जाता है। ढलान को पक्ष में वृद्धि के रूप में परिभाषित किया गया है, या y में परिवर्तन को x में परिवर्तन से विभाजित किया गया है।
- b को "y-अवरोधन" के रूप में परिभाषित किया गया है। Y-अवरोधन वह बिंदु है जहाँ रेखा Y-अक्ष को काटती है।
- x और y चर हैं। आप एक विशिष्ट x मान के लिए हल कर सकते हैं, उदाहरण के लिए, यदि आपके पास एक बिंदु y है और m और b के मान जानते हैं। हालाँकि, x का कभी भी केवल एक मान नहीं होता है: जैसे ही रेखा ऊपर या नीचे जाती है, इसका मान बदल जाता है।
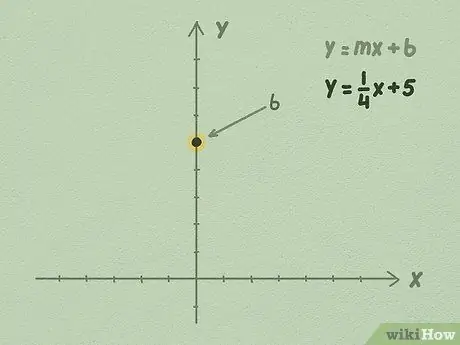
चरण 2. Y अक्ष पर संख्या b खींचिए।
आपका b मान हमेशा एक परिमेय संख्या होगी। जो भी संख्या b है, उसका मान Y अक्ष पर ज्ञात करें, और संख्या को ऊर्ध्वाधर अक्ष पर एक बिंदु पर रखें।
उदाहरण के लिए, आइए समीकरण y = 1/4x + 5 का उपयोग करें। चूंकि अंतिम संख्या b है, हम जानते हैं कि b 5 के बराबर है। Y अक्ष पर 5 अंक ऊपर जाएं और बिंदुओं को चिह्नित करें। यह वह जगह है जहाँ आपकी सीधी रेखा Y अक्ष को काटेगी।
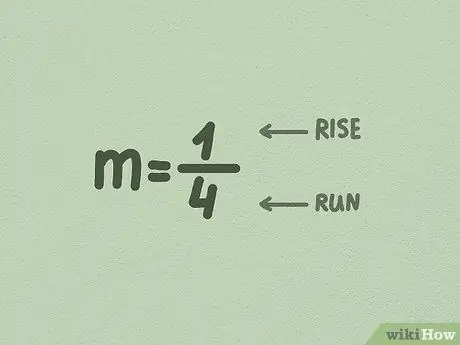
चरण 3. m को भिन्न में बदलें।
अक्सर, x के सामने की संख्या पहले से ही एक भिन्न होती है, इसलिए आपको इसे बदलने की आवश्यकता नहीं होती है। लेकिन यदि नहीं, तो संख्या 1 के नीचे m का मान रखकर बस इसे बदल दें।
- पहली संख्या (अंश) भुजा से विभाजित आरोही में वृद्धि है। यह संख्या इंगित करती है कि रेखा कितनी दूर तक जाती है, या लंबवत रूप से।
- दूसरी संख्या (हर) आरोही में भुजा से विभाजित भुजा है। यह संख्या इंगित करती है कि रेखा कितनी दूर बग़ल में, या क्षैतिज रूप से चलती है।
- उदाहरण के लिए:
- 4/1 का ढलान प्रत्येक 1 बिंदु के पक्ष में 4 अंक ऊपर ले जाता है।
- -2/1 का ढलान प्रत्येक 1 बिंदु के पक्ष में 2 अंक नीचे ले जाता है।
- 1/5 की ढलान प्रत्येक 5 अंक के पक्ष में 1 अंक ऊपर ले जाती है।
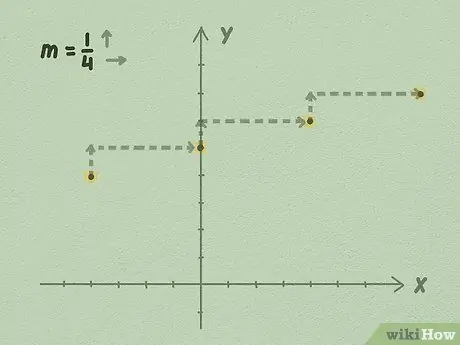
चरण 4। ढलान का उपयोग करके या किनारे से विभाजित करके बी से रेखा का विस्तार करना शुरू करें।
अपने b मान से शुरू करें: हम जानते हैं कि समीकरण इस बिंदु से आगे निकल जाता है। समीकरण में अंक प्राप्त करने के लिए अपनी ढलान लेकर और इसके मूल्य का उपयोग करके रेखा को बढ़ाएं।
- उदाहरण के लिए, ऊपर दिए गए उदाहरण का उपयोग करके, आप देख सकते हैं कि प्रत्येक 1 बिंदु ऊपर के लिए, रेखा 4 बिंदुओं को दाईं ओर ले जाती है। ऐसा इसलिए होता है क्योंकि रेखा का ढलान 1/4 है। आप रेखा को दोनों पक्षों तक अनिश्चित काल तक बढ़ाते हैं, रेखा को ग्राफ़ करने के लिए पक्ष से विभाजित अप का उपयोग करना जारी रखते हैं।
- ऊपर जाने पर ढाल धनात्मक होती है, जबकि नीचे जाने पर ढाल ऋणात्मक होती है। उदाहरण के लिए -1/4 का ढलान, प्रत्येक 4 बिंदुओं के लिए 1 अंक नीचे की ओर जाएगा।
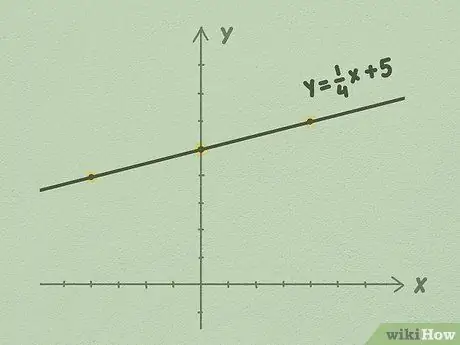
चरण 5. एक रूलर का उपयोग करते हुए रेखा का विस्तार करना जारी रखें और सुनिश्चित करें कि ढलान, m, को एक गाइड के रूप में उपयोग करना सुनिश्चित करें।
रेखा को अनिश्चित काल तक बढ़ाएँ और आप अपने रैखिक समीकरण का रेखांकन कर चुके हैं। बहुत आसान है, है ना?







