जब तक आप अन्य दो कोणों की माप जानते हैं, त्रिभुज का तीसरा कोण खोजना आसान है। आपको बस दोनों कोणों के योग को 180 डिग्री से घटाना है। हालाँकि, ऐसे अन्य तरीके भी हैं जिनका उपयोग करके आप त्रिभुज का तीसरा कोण ज्ञात कर सकते हैं यदि समस्या का आकार सामान्य से थोड़ा अलग है। यदि आप जानना चाहते हैं कि त्रिभुज का तीसरा कोण कैसे ज्ञात किया जाए, तो नीचे दी गई मार्गदर्शिका का पालन करें।
कदम
3 में से विधि 1 अन्य दो कोणों के मापों का उपयोग करना
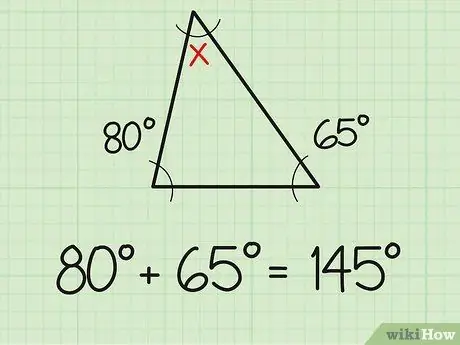
चरण 1. दो ज्ञात कोणों को जोड़ें।
एक तथ्य जो आपको पता होना चाहिए वह यह है कि त्रिभुज के तीनों कोणों का योग हमेशा 180 डिग्री होता है। इसलिए, यदि आप पहले से ही त्रिभुज के दो कोणों का माप जानते हैं, तो तीसरा कोण खोजना उतना ही सरल होगा जितना कि साधारण जोड़ और घटाव के प्रश्न करना। सबसे पहले, उन दो कोण मापों को जोड़ें जिन्हें आप पहले से जानते हैं। उदाहरण के लिए, दो ज्ञात कोण 80 और 65 डिग्री मापते हैं। दोनों को एक साथ जोड़ें (80+65), और आपको 145 डिग्री मिलता है।
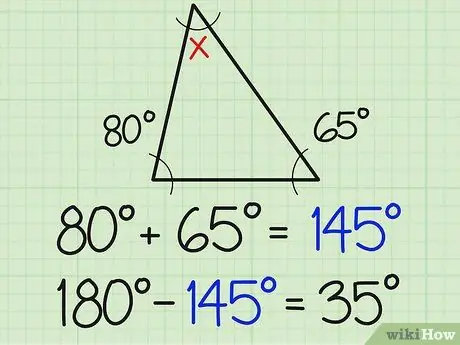
चरण 2. उस संख्या को 180 से विभाजित करें।
त्रिभुज के तीनों कोणों का योग हमेशा 180 डिग्री होता है। इसलिए, कोण के दो ज्ञात मापों के योग में जोड़ने पर तीसरा कोण 180 होना चाहिए। ऊपर के उदाहरण में, इसका मतलब 180-154=35 है।

चरण 3. अपना उत्तर लिखें।
अब आपके पास तीसरे कोण का उत्तर है (उदाहरण 35 डिग्री में)। अगर आपको अभी भी संदेह है, तो खुद देखें। तीन कोणों को एक साथ जोड़ें, और आपको 180 का परिणाम मिलना चाहिए। यदि आप नहीं करते हैं, तो आपकी गणना गलत है। इस उदाहरण के लिए, 80+65+35=180। अगर यह सही है, तो इसका मतलब है कि आपने समस्या हल कर ली है।
विधि २ का ३: चर का उपयोग करना
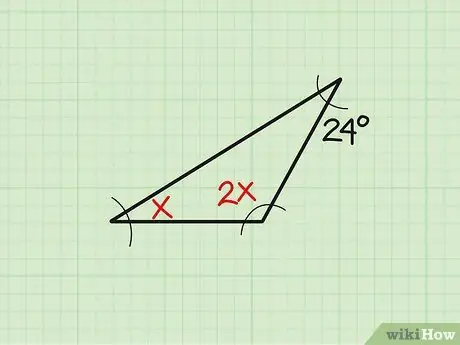
चरण 1. समस्या लिखिए।
कभी-कभी, मौजूदा कोण का आकार एक चर रूप में दिखाया जाता है। आइए इस उदाहरण को लें: "एक त्रिभुज का कोण "x" ज्ञात करें यदि तीन कोण क्रमशः "x", "2x", और 24 मापते हैं। सबसे पहले, समस्या लिखें।

चरण 2. सभी कोण मापों को जोड़ें।
आपको जो सिद्धांत याद रखना चाहिए वह वही रहता है। तो, पहले समस्या में तीन कोणों को जोड़ दें, अर्थात् "x+2x+24 = 3x+24"।
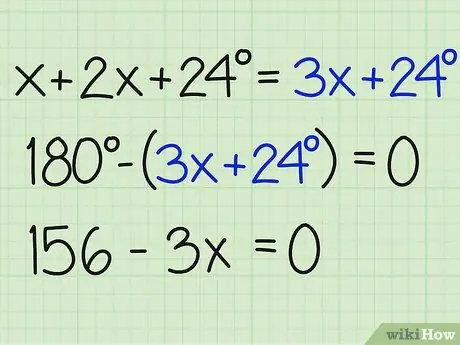
चरण 3. कोणों के योग को 180 से विभाजित करें।
अब, x को खोजने के लिए उस संख्या में 180 डिग्री का अंतर करें और समस्या का उत्तर ज्ञात करें। सुनिश्चित करें कि आपने समीकरण को शून्य के बराबर समाप्त कर दिया है। यहां बताया गया है कि यह कैसे लिखा जाता है:
- 180-(3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
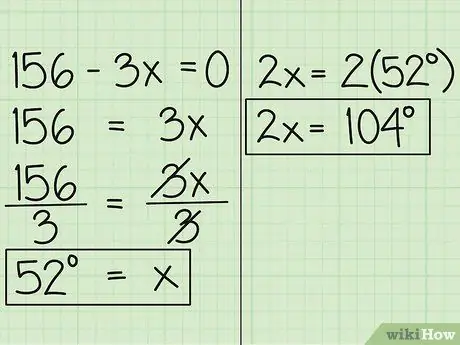
चरण 4. x का मान ज्ञात कीजिए।
अब, चर को समीकरण के दूसरी तरफ ले जाएँ, और आपको 156 = 3x मिलेगा। फिर, समीकरण को 3 से विभाजित करें, तो आपको x = 52 मिलता है। इसका मतलब है कि x में व्यक्त कोण का माप 52 डिग्री है। दूसरा कोण, जिसे 2x में व्यक्त किया गया है, 52 डिग्री गुणा 2 है, जो कि 104 डिग्री है।

चरण 5. अपने परिणामों की जाँच करें।
यदि आप यह सुनिश्चित करना चाहते हैं कि आपका उत्तर सही है, तो बस उन तीन कोण मापों को जोड़ें जिनका उत्तर आपको पहले ही मिल गया है। यदि परिणाम 180 है, तो इसका अर्थ है कि आपका उत्तर सही है। इस उदाहरण के लिए, 52+104+24 = 180।
विधि 3 में से 3: अन्य विधियों का उपयोग करना
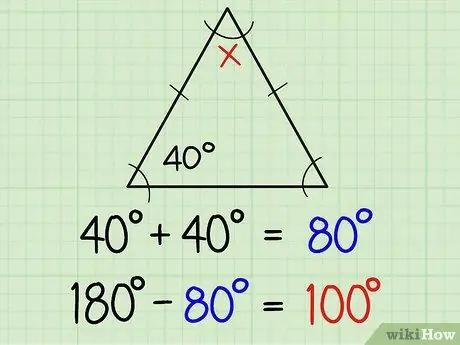
चरण 1. एक समद्विबाहु त्रिभुज के कोण ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज में दो समान भुजाएँ और दो समान कोण होते हैं। दो समान भुजाओं को आमतौर पर पार्श्व रेखा के मध्य में एक छोटी रेखा से चिह्नित किया जाता है, जिसका अर्थ है कि रेखा पर दो विपरीत कोण समान माप हैं। यदि आप पहले से ही एक कोण का आकार जानते हैं, तो आप स्वचालित रूप से दूसरे कोण को जानते हैं। यहां और स्पष्टीकरण दिया गया है:
यदि समान कोणों में से एक 40 डिग्री है, तो दूसरा 40 डिग्री है। इस तरह आप सभी तीन कोणों को 40+40 (यानी 80) और 180 के योग के बीच के अंतर के साथ, या दूसरे शब्दों में 180-80 = 100 के रूप में पा सकते हैं।
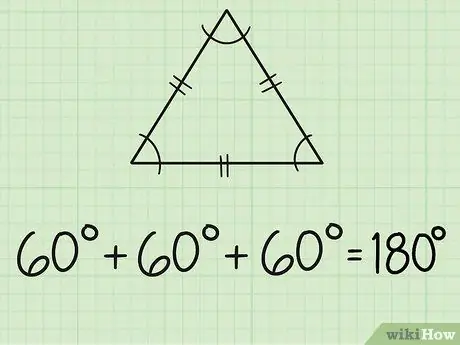
चरण 2. एक समबाहु त्रिभुज के कोण ज्ञात कीजिए।
एक समबाहु त्रिभुज में तीन समान भुजाएँ और तीन समान कोण होते हैं। प्रत्येक पक्ष को आमतौर पर बीच में दो छोटी रेखाओं से चिह्नित किया जाता है। चूँकि तीनों कोण बराबर हैं, इसका मतलब है कि सभी कोणों की माप 60 डिग्री है, क्योंकि 180/3 = 60.

चरण 3. एक समकोण त्रिभुज में तीसरा कोण ज्ञात कीजिए।
मान लीजिए कि आपको एक समकोण त्रिभुज मिलता है, जिसमें से एक न्यून कोण 30 डिग्री मापता है। चूंकि त्रिभुज एक समकोण है, इसका मतलब है कि कोणों में से एक, अर्थात् समकोण, को 90 डिग्री मापना चाहिए। फिर त्रिभुज सिद्धांत का प्रयोग करें, दो कोणों (90+30 = 120) के योग के बीच का अंतर 180 से करें, तो आपको 180-120 = 60 डिग्री मिलेगा।







