दशमलव संख्याओं से विभाजित करना पहली बार में मुश्किल लगता है क्योंकि किसी ने भी आपको "0, 7 टाइम्स टेबल" नहीं सिखाया है। ऐसा करने का रहस्य विभाजन की समस्या को एक ऐसे प्रारूप में बदलना है जो केवल पूर्ण संख्याओं का उपयोग करता है। इस तरह से समस्या को फिर से लिखने के बाद, यह एक नियमित लंबी विभाजन समस्या बन जाएगी।
कदम
भाग 1 का 2: साधारण विभाजन समस्याओं के रूप में समस्याओं को लिखना
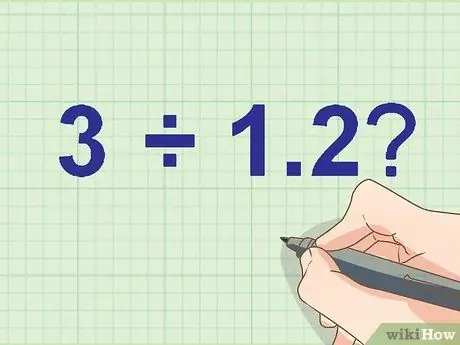
चरण 1. अपनी विभाजन समस्या लिखिए।
अगर आप अपने काम में सुधार करना चाहते हैं तो पेंसिल का इस्तेमाल करें।
-
उदाहरण:
कितने 3 ÷ 1, 2?

चरण 2. पूर्ण संख्या को दशमलव के रूप में लिखें।
पूर्ण संख्या के बाद दशमलव बिंदु लिखें, फिर दशमलव बिंदु के बाद शून्य लिखें। ऐसा तब तक करें जब तक कि दोनों संख्याओं का दशमलव बिंदु के दाईं ओर एक ही स्थान मान न हो। यह पूर्णांक मान नहीं बदलता है।
-
उदाहरण:
समस्या ३ १, २ में हमारी पूर्ण संख्या ३ है। चूँकि १, २ का दशमलव बिंदु के दाईं ओर एक स्थानीय मान है, ३ को ३, ० के रूप में लिखें ताकि इस संख्या का भी दशमलव के बाद एक स्थानीय मान हो। अब हमारी बात बन जाती है 3, 0 ÷ 1, 2.
- चेतावनी: दशमलव बिंदु के बाईं ओर शून्य न जोड़ें! संख्या ३, ३, ० या ३, ०० के बराबर है, लेकिन ३० या ३०० के बराबर नहीं है।

चरण 3. दशमलव बिंदु को दाईं ओर ले जाएं जब तक कि आपको एक पूर्ण संख्या न मिल जाए।
भाग की समस्याओं में, आप दशमलव बिंदुओं को स्थानांतरित कर सकते हैं, लेकिन केवल तभी जब आप सभी संख्याओं पर दशमलव बिंदुओं को समान चरणों में स्थानांतरित करते हैं। यह आपको समस्या को पूर्ण संख्या में बदलने की अनुमति देता है।
-
उदाहरण:
3, 0 1, 2 को पूर्ण संख्या में बदलने के लिए, दशमलव बिंदु को एक कदम दाईं ओर ले जाएँ। इस प्रकार, 3, 0 30 हो जाता है और 1, 2 12 हो जाता है। अब, हमारी समस्या बन जाती है 30 ÷ 12.

चरण 4. दीर्घ भाग का प्रयोग करते हुए समस्या लिखिए।
विभाज्य संख्या (आमतौर पर बड़ी संख्या) को लंबे विभाजन चिह्न के नीचे रखें। इस चिन्ह के बाहर भाजक संख्या लिखिए। अब, आपके पास एक नियमित लंबी विभाजन समस्या है जो पूर्ण संख्याओं का उपयोग करती है। यदि आप लंबे विभाजन को कैसे करें, इस पर अनुस्मारक चाहते हैं, तो अगला भाग पढ़ें।
भाग 2 का 2: लंबी डिवीजन की समस्याओं को हल करना

चरण 1. उत्तर का पहला अंक ज्ञात कीजिए।
भाजक और विभाजित संख्या के पहले अंक की तुलना करके इस समस्या को उसी तरह हल करना शुरू करें जैसे आप सामान्य रूप से करते हैं। इस पहले अंक को भाजक की संख्या से विभाजित करने के परिणाम की गणना करें, फिर उस अंक के ऊपर परिणाम लिखें।
उदाहरण: हम 30 को 12 से विभाजित करने का प्रयास कर रहे हैं। 12 की तुलना संख्या के पहले अंक से करें, जो कि 3 है। चूंकि 12 3 से बड़ा है, 3 को 12 से विभाजित 0 के बराबर है। 0 उत्तर पंक्ति में 3 से ऊपर।
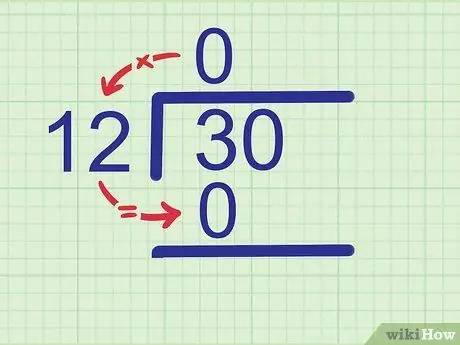
चरण 2. भागफल को भाजक से गुणा करें।
विभाजित की गई संख्या के अंतर्गत उत्पाद का गुणनफल लिखें। आपके द्वारा विभाजित संख्या के पहले अंक के ठीक नीचे परिणाम लिखें क्योंकि यह वह अंक है जिसे आपने अभी देखा है।
-
उदाहरण:
चूँकि 0 x 12 = 0, लिखिए 0 3 के तहत
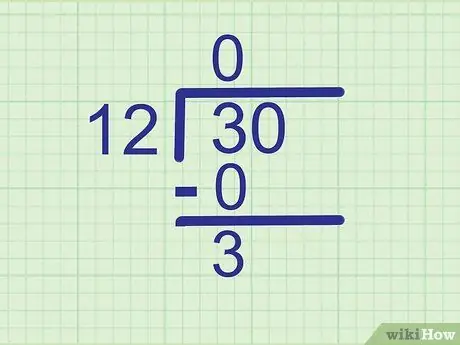
चरण 3. शेषफल ज्ञात करने के लिए घटाइए।
आपके द्वारा अभी गणना किए गए उत्पाद को सीधे उसके ऊपर के अंक से घटाएं। इसके नीचे एक नई लाइन पर उत्तर लिखें।
-
उदाहरण:
३ - ० = ३, अतः लिखिए
चरण 3। 0 के ठीक नीचे।
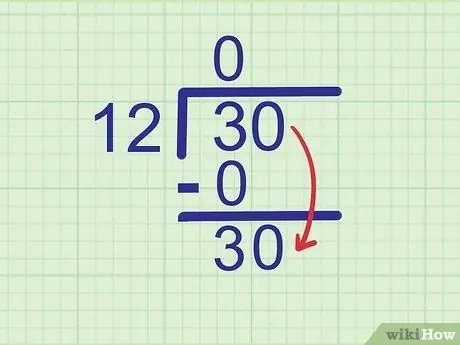
चरण 4. अगला अंक कम करें।
विभाजित संख्या के अगले अंक को उस संख्या के आगे छोड़ दें जिसे आपने अभी लिखा है।
-
उदाहरण:
विभाजित होने वाली संख्या 30 है। हमने संख्या 3 देखी है, इसलिए अगला अंक जिसे कम किया जाना चाहिए वह 0 है। संख्या 0 को 3 के पक्ष में घटाएं ताकि यह बन जाए
चरण 30..
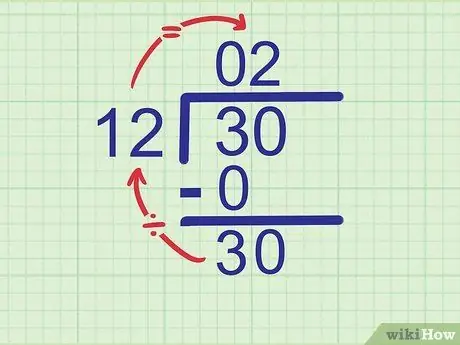
चरण 5. नई संख्या को भाजक से विभाजित करने का प्रयास करें।
अब, अपने उत्तर का दूसरा अंक खोजने के लिए इस खंड के पहले चरण को दोहराएं। इस बार, भाजक की तुलना उस संख्या से करें जिसे आपने अभी नीचे की पंक्ति में लिखा है।
-
उदाहरण:
30 बटा 12 का भागफल क्या है? निकटतम उत्तर हम 2 प्राप्त कर सकते हैं क्योंकि 12 x 2 = 24. लिखें
चरण 2। उत्तर पंक्ति में दूसरे स्थान पर।
- यदि आप उत्तर के बारे में सुनिश्चित नहीं हैं, तब तक कई गुणा करने का प्रयास करें जब तक कि आपको सबसे बड़ा उत्तर फिट न हो जाए। उदाहरण के लिए, यदि आपका अनुमान ३ है, तो १२ x ३ की गणना करें और आपको ३६ प्राप्त होता है। यह संख्या बहुत बड़ी है क्योंकि हम ३० की गणना करने की कोशिश कर रहे हैं। एक संख्या को कम करने का प्रयास करें, १२ x २ = २४। यह संख्या फिट बैठती है। तो, 2 सही उत्तर है।

चरण 6. अगली संख्या ज्ञात करने के लिए उपरोक्त चरणों को दोहराएँ।
यह वही लंबी विभाजन प्रक्रिया है जैसा कि ऊपर इस्तेमाल किया गया है, और किसी भी लंबी विभाजन समस्या के लिए:
- अपने उत्तर के नए अंक को भाजक से गुणा करें: 2 x 12 = 24.
- विभाजित की गई संख्या के नीचे उत्पाद को एक नई लाइन पर लिखें: 30 के ठीक नीचे 24 लिखें।
- नीचे की पंक्ति को ऊपर की पंक्ति से घटाएँ: 30 - 24 = 6. इसलिए, इसके नीचे एक नई पंक्ति में 6 लिखें।

चरण 7. इस प्रक्रिया को तब तक जारी रखें जब तक आप उत्तर की अंतिम पंक्ति को पूरा नहीं कर लेते।
यदि विभाजित संख्या में अभी भी अंक शेष हैं, तो अंकों को नीचे करें और उसी तरह से समस्या को हल करना जारी रखें। यदि आपने उत्तर की अंतिम पंक्ति पूरी कर ली है, तो अगले चरण पर जारी रखें।
-
उदाहरण:
हमने अभी लिखा
चरण 2। अंतिम उत्तर पंक्ति में। अगले चरण पर आगे बढ़ें।

चरण 8. यदि आवश्यक हो तो विभाजित संख्या को "विस्तारित" करने के लिए दशमलव जोड़ें।
यदि संख्या समान रूप से विभाज्य है, तो आपका अंतिम घटाव परिणाम "0" है। इसका मतलब है, आपने विभाजित करना समाप्त कर दिया है और आपको एक पूर्ण संख्या के रूप में उत्तर मिलता है। हालाँकि, यदि आपने उत्तरों की अंतिम पंक्ति को पूरा कर लिया है और अभी भी ऐसे अंक हैं जिन्हें विभाजित किया जा सकता है, तो आपको दशमलव बिंदु के बाद संख्या 0 जोड़कर विभाज्य संख्या को "विस्तारित" करना होगा। ध्यान रखें कि यह संख्या का मान न बदलें।
-
उदाहरण:
हम उत्तर की अंतिम पंक्ति पर आ गए हैं, लेकिन हमारे अंतिम घटाव का उत्तर "6" है। लांग डिविजन सिंबल के नीचे अंतिम अंक में ",0" जोड़कर "6,0" लिखें। उत्तर रेखा पर दशमलव बिंदु भी उसी स्थान पर लिखें, लेकिन उसके बाद कुछ भी न लिखें।

चरण 9. अगले अंक को खोजने के लिए समान चरणों को दोहराएं।
यहां फर्क सिर्फ इतना है कि आपको उत्तर रेखा पर दशमलव बिंदु को उसी स्थान पर जोड़ना है। एक बार जब आप ऐसा कर लेते हैं, तो आप ठीक उसी तरह शेष उत्तर अंकों की खोज कर सकते हैं।
-
उदाहरण:
नई 0 को अंतिम पंक्ति में नीचे गिराएं ताकि यह "60" हो जाए। चूँकि ६० को १२ से भाग देने पर ठीक ५ होता है, लिखो
चरण 5. हमारी उत्तर पंक्ति के अंतिम अंक के रूप में। यह न भूलें कि हम अपनी उत्तर पंक्ति में दशमलव लगाते हैं। इसलिए, 2, 5 हमारे प्रश्न का अंतिम उत्तर है।
टिप्स
- आप इसे शेषफल के रूप में लिख सकते हैं (इसलिए 3 1, 2 का उत्तर "2 शेष 6" है)। हालाँकि, क्योंकि आप दशमलव के साथ काम कर रहे हैं, आपका शिक्षक आपसे उत्तर के दशमलव भाग पर काम करने की उम्मीद कर सकता है।
- यदि आप लंबी विभाजन विधि का सही ढंग से पालन करते हैं, तो आपके पास हमेशा सही स्थिति में दशमलव बिंदु होगा, या कोई दशमलव बिंदु नहीं होगा यदि संख्या विभाज्य से विभाज्य है। दशमलव स्थानों का अनुमान लगाने की कोशिश न करें। दशमलव स्थान अक्सर आपकी प्रारंभिक संख्या के दशमलव स्थान से भिन्न होता है।
- यदि लंबे विभाजन की समस्या लंबे समय तक नहीं रहती है, तो आप रुक सकते हैं और निकटतम संख्या में चक्कर लगा सकते हैं। उदाहरण के लिए, १७ ४, २ को हल करने के लिए, बस ४.०४७ तक गिनें… और अपने उत्तर को "लगभग 4.05" तक गोल करें।
-
अपने विभाजन की शर्तें याद रखें:
- विभाजित की जाने वाली संख्या विभाजित होने वाली संख्या है।
- भाजक वह संख्या है जिसका उपयोग विभाजित करने के लिए किया जाता है।
- भागफल गणित विभाजन की समस्या का उत्तर है।
- संपूर्ण: भाजक से विभाजित = भागफल।
चेतावनी
याद रखें कि ३० १२ में ३ १, २ के समान उत्तर दिया जाएगा। दशमलव को पीछे की ओर ले जाने के बाद अपने उत्तर को "सही" करने का प्रयास न करें।
संबंधित विकिहाउ लेख
- सामान्य भिन्नों को दशमलव में बदलना
- लंबे समय से निर्धारित डिवीजन करना
- भिन्नों को भिन्नों से विभाजित करें
- मिश्रित भिन्नों को विभाजित करना







