भिन्नों को पूर्ण संख्याओं से विभाजित करना उतना कठिन नहीं है जितना लगता है। एक भिन्न को एक पूर्णांक से विभाजित करने के लिए, आपको केवल पूर्ण संख्या को भिन्न में बदलना है, भिन्न का व्युत्क्रम ज्ञात करना है, और परिणाम को पहले भिन्न से गुणा करना है। यदि आप जानना चाहते हैं कि यह कैसे करना है, तो बस इन चरणों का पालन करें:
कदम
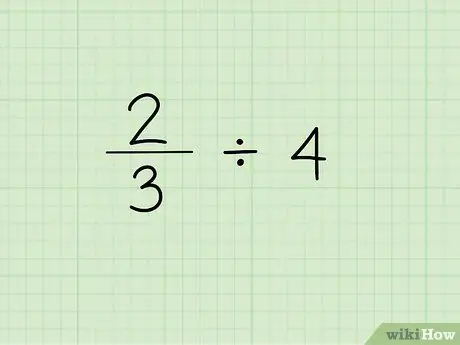
चरण 1. समस्या लिखिए।
किसी भिन्न को पूर्णांक से विभाजित करने का पहला चरण है भिन्न को उसके बाद भाग का चिह्न और उस पूर्णांक को लिखना जो भिन्न को विभाजित करने के लिए आवश्यक है। मान लें कि हम निम्नलिखित समस्या के साथ काम कर रहे हैं: 2/3 4.
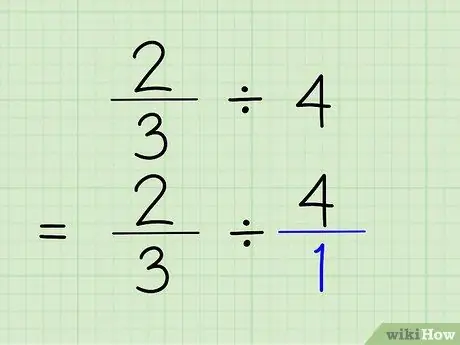
चरण 2. पूर्णांकों को भिन्नों में बदलें।
एक पूर्णांक को भिन्न में बदलने के लिए, आपको केवल पूर्णांक को संख्या 1 के ऊपर रखना है। पूर्णांक अंश बन जाता है और 1 भिन्न का हर बन जाता है। 4/1 कहना वास्तव में 4 कहने जैसा ही है, क्योंकि आप केवल यह दिखा रहे हैं कि संख्या में 4 बार "1" है। समस्या 2/3 4/1 होगी।
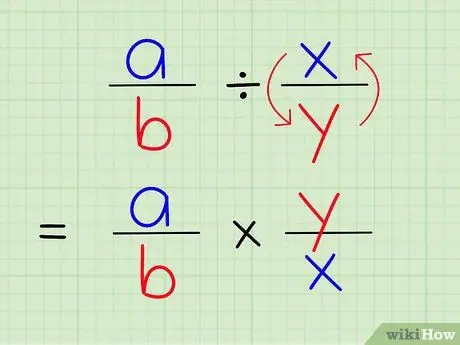
चरण 3. एक भिन्न को दूसरी भिन्न से भाग देना, उस भिन्न को दूसरी भिन्न के व्युत्क्रम से गुणा करने के समान है।
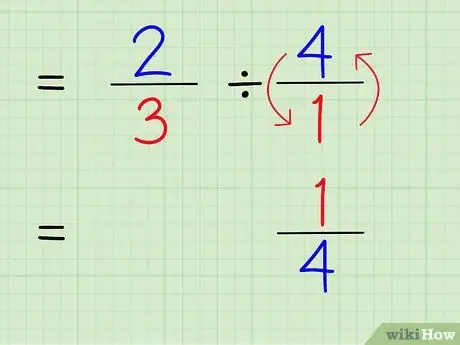
चरण 4. पूर्णांक का व्युत्क्रम लिखिए।
किसी संख्या का व्युत्क्रम ज्ञात करने के लिए, संख्या के अंश और हर को स्वैप करें। इसलिए, 4/1 का व्युत्क्रम ज्ञात करने के लिए, बस अंश और हर को स्वैप करें ताकि संख्या 1/4 हो जाए।
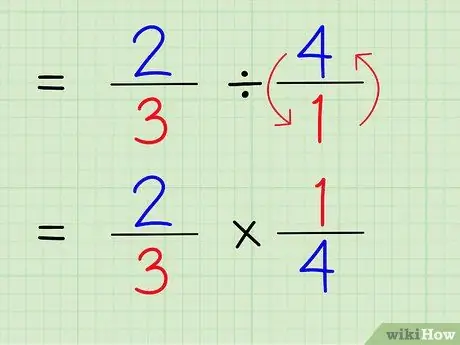
चरण 5. भाग चिह्न को गुणन चिह्न में बदलें।
समस्या 2/3 x 1/4 होगी।
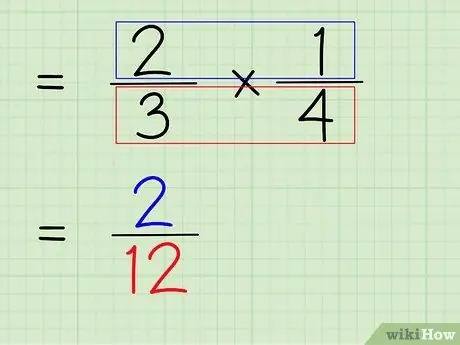
चरण 6. भिन्न के अंश और हर को गुणा करें।
तो, अगला चरण भिन्न के अंश और हर को गुणा करना है ताकि अंतिम उत्तर के रूप में एक नया अंश और हर प्राप्त किया जा सके।
- अंशों को गुणा करने के लिए, 2 प्राप्त करने के लिए बस 2 x 1 गुणा करें।
- हर को गुणा करने के लिए, 12 प्राप्त करने के लिए बस 3 x 4 गुणा करें।
- 2/3 x 1/4 = 2/12
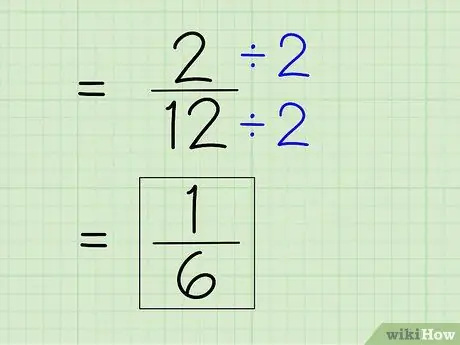
चरण 7. भिन्न को सरल कीजिए।
एक भिन्न को सरल बनाने के लिए, आपको सबसे छोटा हर खोजना होगा, जिसका अर्थ है कि आपको अंश और हर को किसी भी संख्या से विभाजित करना होगा जो दोनों संख्याओं को विभाजित करता है। चूंकि 2 अंश है, आपको देखना होगा कि क्या 2 12 को पूरी तरह से विभाजित कर सकता है - ऐसा इसलिए हो सकता है क्योंकि 12 एक सम संख्या है। फिर, सरल उत्तर प्राप्त करने के लिए एक नया अंश और हर प्राप्त करने के लिए अंश और हर को 2 से विभाजित करें।
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- भिन्न 2/12 को 1/6 तक सरल बनाया जा सकता है। यह आपका अंतिम उत्तर है।
टिप्स
- यह स्मृति की सहायता करना है, यह याद रखने का एक आसान तरीका है कि इन सभी गणनाओं को कैसे किया जाए। इसे ध्यान में रखें: "अंशों को विभाजित करना, दूसरी संख्या को उलटना और गुणा करना आसान है!"
- उपरोक्त विधि का एक अन्य रूप JGB/JBG है। पहला नंबर मत बदलो। गुणन में बदलें। अंतिम संख्या को उलट दें। या B पहले फिर G.
- यदि आप गणना को गुणा करने से पहले रद्द कर देते हैं, तो आपको भिन्न का सबसे सरल रूप खोजने की आवश्यकता नहीं हो सकती है क्योंकि परिणाम पहले से ही सबसे सरल भिन्न रूप में है जैसा कि आप देख सकते हैं। हमारे उदाहरण में, 2/3 × 1/4 गुणा करने से पहले, हम देख सकते हैं कि पहले अंश (2) और दूसरे हर (4) में 2 का समान गुणक है, जिसे हम गणना जारी रखने से पहले रद्द कर सकते हैं। यह समस्या को 1/3 × 1/2 में बदल देता है, जो तत्काल 1/6 परिणाम देता है और बाद के चरण में भिन्न को सरल बनाने में हमारा समय बचाता है।
- यदि आपकी भिन्नों में से कोई एक ऋणात्मक है, तो यह विधि अभी भी व्यावहारिक है; सुनिश्चित करें कि आप इन चरणों का पालन करते हुए संकेतों का ट्रैक रखते हैं।







