एक समचतुर्भुज एक चतुर्भुज होता है जिसकी चार बराबर भुजाएँ होती हैं। समचतुर्भुज का क्षेत्रफल ज्ञात करने के तीन सूत्र हैं। कैसे जानने के लिए बस इन चरणों का पालन करें।
कदम
विधि 1 में से 3: विकर्ण का उपयोग करना
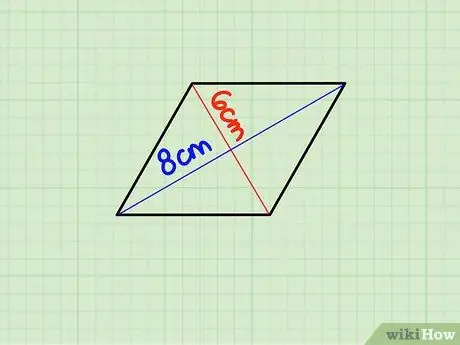
चरण 1. प्रत्येक विकर्ण की लंबाई ज्ञात कीजिए।
एक समचतुर्भुज के विकर्ण आकृति के केंद्र में विपरीत शीर्षों (कोनों) को जोड़ने वाली रेखाएँ हैं। एक समचतुर्भुज के विकर्ण लंबवत होते हैं और प्रतिच्छेदन बिंदु से होकर चार समकोण त्रिभुज बनाते हैं।
मान लीजिए कि विकर्ण 6 सेमी है और लंबाई 8 सेमी है।
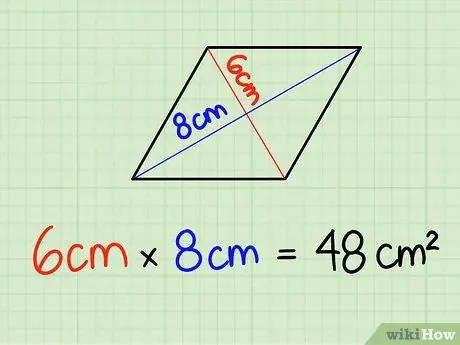
चरण 2. विकर्ण की लंबाई गुणा करें।
बस विकर्ण की लंबाई लिखिए और गुणा कीजिए। इस स्थिति में, 6 सेमी x 8 सेमी = 48 सेमी2. इकाइयों को गुणा करना न भूलें क्योंकि हम वर्ग इकाइयों के साथ काम कर रहे हैं।
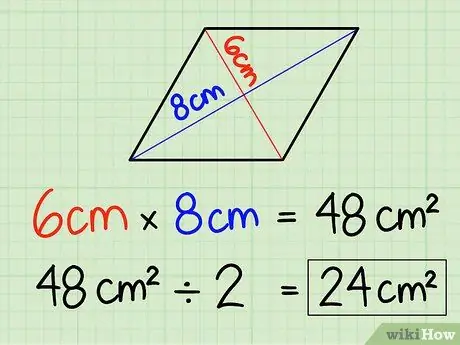
चरण 3. परिणाम को 2 से विभाजित करें।
क्योंकि 6 सेमी x 8 सेमी = 48 सेमी2, बस परिणाम को 2.48 सेमी. से विभाजित करें2/2 = 24 सेमी2. एक समचतुर्भुज का क्षेत्रफल 24 सेमी. है2.
विधि २ का ३: आधार और ऊँचाई का उपयोग करना
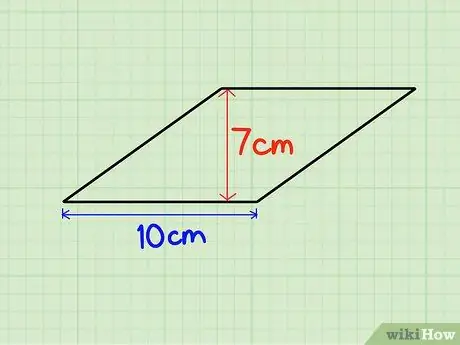
चरण 1. आधार और ऊँचाई ज्ञात कीजिए।
हम समचतुर्भुज की ऊँचाई को समचतुर्भुज की भुजा की लंबाई से भी गुणा कर सकते हैं। मान लीजिए कि समचतुर्भुज की ऊंचाई 7 सेमी और आधार 10 सेमी है।
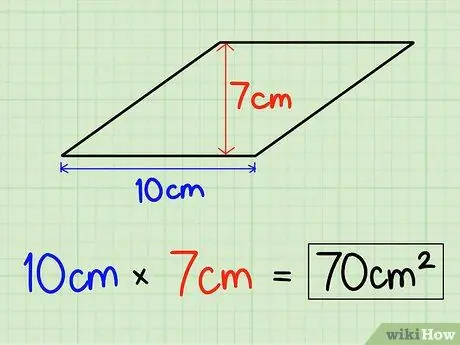
चरण 2. आधार और ऊंचाई को गुणा करें।
समचतुर्भुज का आधार और ऊँचाई जानने के बाद उसे गुणा करके उसका क्षेत्रफल ज्ञात कीजिए। तो, 10 सेमी x 7 सेमी = 70 सेमी2. एक समचतुर्भुज का क्षेत्रफल 70 सेमी. है2.
विधि 3 का 3: त्रिकोणमिति का उपयोग करना
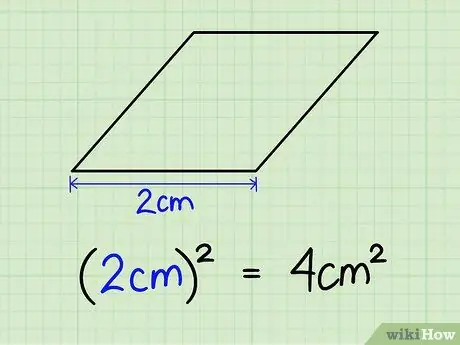
चरण 1. किसी भी भुजा की लंबाई को चौकोर करें।
एक समचतुर्भुज की चार बराबर भुजाएँ होती हैं, इसलिए इससे कोई फ़र्क नहीं पड़ता कि हम किस पक्ष को चुनते हैं। मान लीजिए कि भुजा की लंबाई 2 सेमी है। 2 सेमी x 2 सेमी = 4 सेमी2.

चरण 2. एक कोने की ज्या से गुणा करें।
इससे कोई फर्क नहीं पड़ता कि हम कौन सा कोण चुनते हैं। मान लीजिए कि इनमें से एक कोण 33 डिग्री है। बस ज्या (33) को 4 सेमी. से गुणा करें2 समचतुर्भुज का क्षेत्रफल ज्ञात करने के लिए। (2 सेमी)2 एक्स साइन (33) = 4 सेमी2 x 1 = 4 सेमी2. एक समचतुर्भुज का क्षेत्रफल 4 सेमी. है2.







