फ्लैट आकार के कई अलग-अलग आकार हैं और कई कारण हैं कि आप क्षेत्र की गणना क्यों करना चाहते हैं: गृहकार्य करने से यह अनुमान लगाने के लिए कि रहने वाले कमरे को फिर से रंगने के लिए कितने रंग की आवश्यकता है। चिंता न करें, विकिहाउ के पास इसका जवाब है! समतल आकृति के क्षेत्रफल की गणना कैसे करें, यह जानने के लिए नीचे चरण 1 से प्रारंभ करें।
कदम
विधि 1 का 7: वर्ग, आयत और समांतर चतुर्भुज
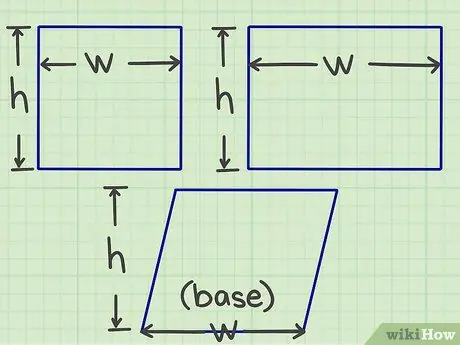
चरण 1. लंबाई और चौड़ाई को मापें।
समतल आकार की लंबाई और चौड़ाई को मापना या पता लगाना शुरू करें (या दूसरे शब्दों में, एक बिंदु पर मिलने वाली दो भुजाओं में से प्रत्येक का आकार)।
- एक समांतर चतुर्भुज के लिए, आपको आधार और ऊँचाई ज्ञात करनी होती है, लेकिन सरल शब्दों में, विचार लंबाई और चौड़ाई के समान होता है।
- वास्तविक दुनिया में, आपको इसे स्वयं मापने की आवश्यकता हो सकती है, लेकिन जब गृहकार्य करने की बात आती है, तो शिक्षक आमतौर पर आकृति की तस्वीर के साथ संख्याएं लिख चुका होता है।
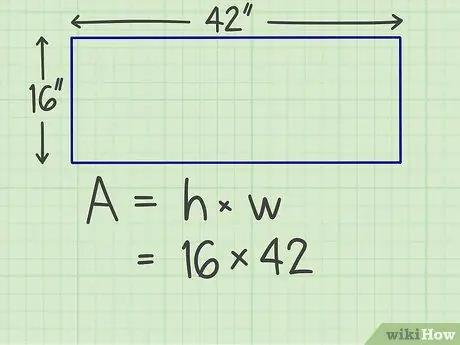
चरण 2. पक्षों को गुणा करें।
एक तरफ से दूसरी तरफ गुणा करें। उदाहरण के लिए, मान लें कि आपके पास 16 इंच की चौड़ाई और 42 इंच की लंबाई वाला एक आयत है, तो आपको 16 x 42 की गणना करनी होगी।
यदि आप एक वर्ग (पूर्व में एक वर्ग) के क्षेत्र की गणना कर रहे हैं, तो कैलकुलेटर का उपयोग करके इसके एक पक्ष को वर्ग करके समय बचाएं। यदि भुजा 4 मीटर मापती है, तो 4 कुंजी दबाएं और फिर परिणाम प्रदर्शित करने के लिए कैलकुलेटर पर वर्गाकार कुंजी दबाएं। वर्ग का अर्थ है किसी संख्या को अपने आप से गुणा करना।
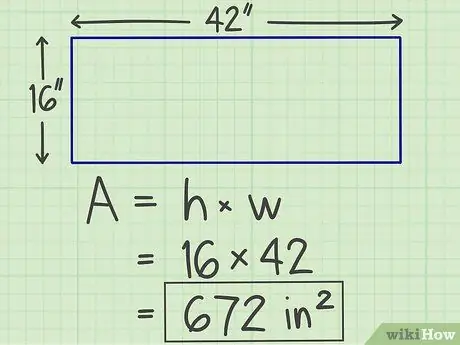
चरण 3. परिणाम लिखें।
आपके द्वारा पहले किया गया गुणन एक संख्या उत्पन्न करेगा, जो कि उस विमान का क्षेत्रफल है जिसकी आप गणना कर रहे हैं, इकाई "वर्ग" के साथ। इस प्रकार, हमने पहले जिस आयत की गणना की, उसका क्षेत्रफल 672 वर्ग इंच है।
कभी-कभी इस वर्ग इकाई को छोटे 2 के रूप में भी लिखा जाता है जो इकाई के नाम (जैसे लेखन शक्ति) के बाद थोड़ा ऊपर उठता है।
विधि २ का ७: ट्रेपेज़ॉइड
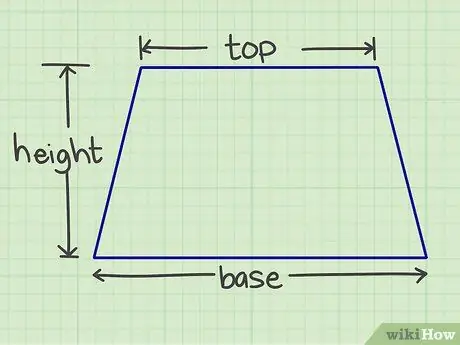
चरण 1. आवश्यक संख्या को मापें।
आपको आधार, छत और ऊंचाई को मापने की आवश्यकता होगी। आधार और छत समानांतर भुजाएँ हैं, जबकि ऊँचाई दो समानांतर भुजाओं को जोड़ने वाली एक लंबवत रेखा है।
वास्तविक दुनिया में, आपको इसे स्वयं मापने की आवश्यकता हो सकती है, लेकिन जब गृहकार्य करने की बात आती है, तो शिक्षक आमतौर पर आकृति की तस्वीर के साथ संख्याएं लिख चुका होता है।
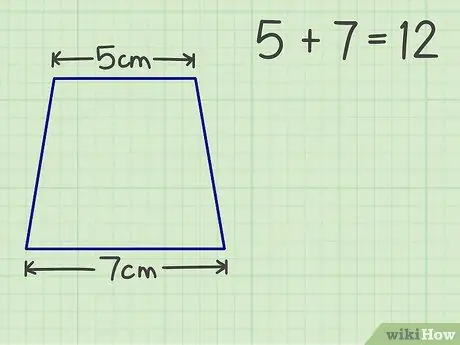
चरण 2. दो समानांतर भुजाओं को जोड़ें।
उदाहरण के लिए, हमारे समलम्ब चतुर्भुज की छत 5 सेमी और आधार 7 सेमी है। दो समांतर भुजाओं का योग 12 है।
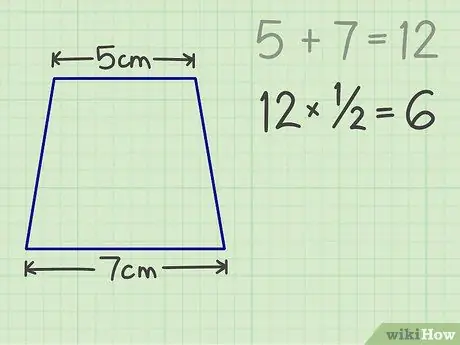
चरण 3. संख्या को 1/2 से गुणा करें, परिणाम 6 है।
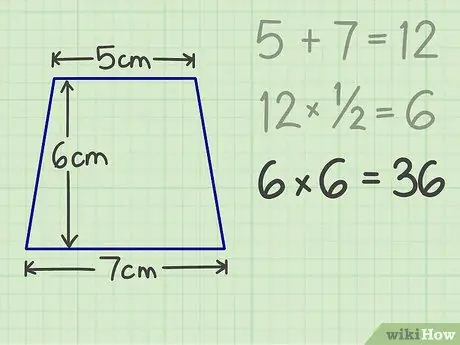
चरण 4. उसके बाद परिणाम को ऊंचाई से गुणा करें।
उदाहरण के लिए, यदि एक ट्रेपेज़ॉइड की ऊंचाई 6 सेमी है, तो अंतिम परिणाम 36 है।
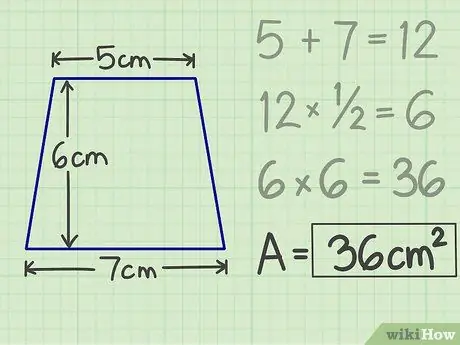
चरण 5. परिणाम लिखें।
आपने पहले जो गुणन किया था वह एक संख्या उत्पन्न करेगा, अर्थात् समलम्ब का क्षेत्रफल। तो 5 सेमी की छत, 7 सेमी के आधार और 6 सेमी की ऊंचाई के साथ एक समलम्ब चतुर्भुज के लिए, क्षेत्रफल 36 सेमी वर्ग है।
विधि ३ का ७: वृत्त
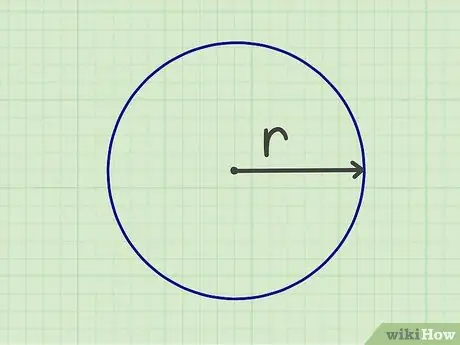
चरण 1. त्रिज्या को मापें।
एक वृत्त के क्षेत्रफल की गणना करने में सक्षम होने के लिए, आपको त्रिज्या को मापने की आवश्यकता है। त्रिज्या वृत्त के केंद्र से उसके किनारे तक की दूरी है। आप व्यास (किनारे से किनारे तक सर्कल की चौड़ाई) को मापकर त्रिज्या को माप सकते हैं, फिर संख्या को दो से विभाजित कर सकते हैं।
वास्तविक दुनिया में, आपको इसे स्वयं मापने की आवश्यकता हो सकती है, लेकिन जब गृहकार्य करने की बात आती है, तो शिक्षक आमतौर पर आकृति की तस्वीर के साथ संख्याएं लिख चुका होता है।
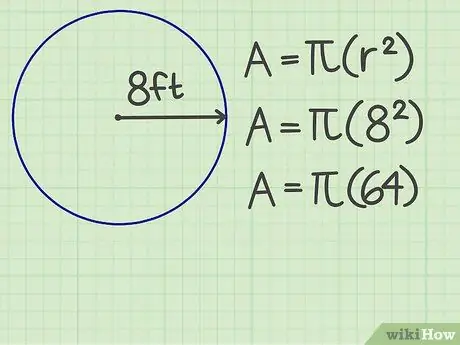
चरण 2. उंगलियों को चौकोर करें।
त्रिज्या की संख्या को स्वयं से गुणा करें। उदाहरण के लिए, एक वृत्त की त्रिज्या 8 फीट है, इसलिए परिणाम 64 है।
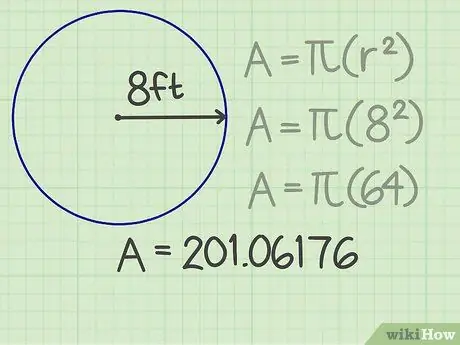
चरण 3. परिणाम को pi से गुणा करें।
पाई (π) विभिन्न सूत्रों में प्रयुक्त एक महत्वपूर्ण संख्या है। यदि आप कैलकुलेटर का उपयोग कर रहे हैं, तो वास्तव में सटीक परिणाम प्राप्त करने के लिए पाई कुंजी दबाएं। अन्यथा, अपनी गणना को आसान बनाने के लिए, आप अल्पविराम के बाद pi को कुछ अंकों में गोल कर सकते हैं, उदाहरण के लिए, 3, 14159। जब आप इस संख्या को त्रिज्या के वर्ग से गुणा करते हैं, तो परिणाम 201, 06176 होता है।
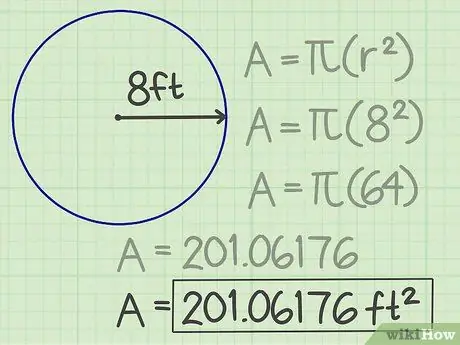
चरण 4. परिणाम लिखिए।
प्राप्त संख्या 201, 06176 वृत्त का क्षेत्रफल है। इस प्रकार इसका क्षेत्रफल 201,06176 वर्ग फुट है।
विधि 4 का 7: सेक्टर (न्यायिक)
चरण 1. आवश्यक संख्याओं को मापें।
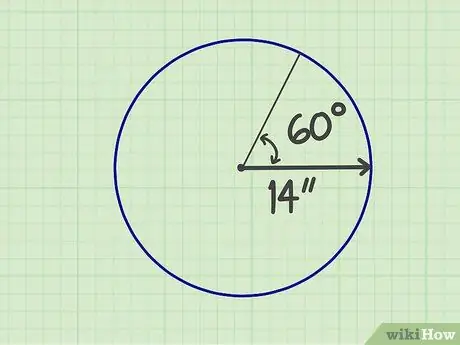
एक त्रिज्यखंड एक वृत्त का एक भाग है जो दो त्रिज्याओं और एक किनारे से बनता है, ताकि आकार एक पंखे की तरह हो। आपको त्रिज्या के आकार और "पंखे" को बनाने वाले कोण को जानना होगा। उदाहरण के लिए, मान लीजिए कि एक त्रिज्यखंड की त्रिज्या 14 इंच और कोण 60 डिग्री है।
वास्तविक दुनिया में, आपको इसे स्वयं मापने की आवश्यकता हो सकती है, लेकिन जब गृहकार्य करने की बात आती है, तो शिक्षक आमतौर पर आकृति की तस्वीर के साथ संख्याएं लिख चुका होता है।
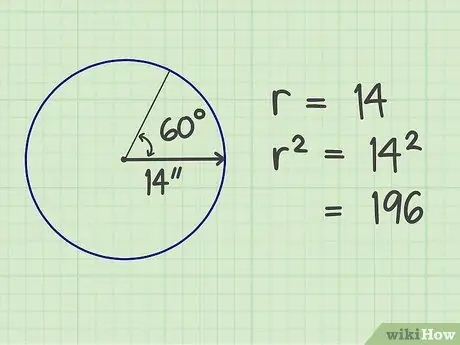
चरण 2. उंगलियों को चौकोर करें।
त्रिज्या की संख्या को स्वयं से गुणा करें। परिणाम 196 (14x14) है।

चरण 3. परिणाम को pi से गुणा करें।
पाई (π) विभिन्न सूत्रों में प्रयुक्त एक महत्वपूर्ण संख्या है। यदि आप कैलकुलेटर का उपयोग कर रहे हैं, तो वास्तव में सटीक परिणाम प्राप्त करने के लिए पाई कुंजी दबाएं। अन्यथा, अपनी गणना को आसान बनाने के लिए, आप अल्पविराम के बाद पाई को कुछ अंकों में गोल कर सकते हैं, उदाहरण के लिए 3, 14159। यदि आप इस संख्या को त्रिज्या के वर्ग से गुणा करते हैं, तो परिणाम 615, 75164 है।

चरण 4. कोण के माप को 360 से विभाजित करें।
सेक्टर फैन एंगल को 360 (एक फुल सर्कल एंगल का माप) से विभाजित करें। ऊपर के उदाहरण के लिए, परिणाम लगभग 0.166 है। यदि आप इसे कैलकुलेटर के साथ गणना करते हैं, तो परिणाम वास्तव में लंबा और पुनरावृत्त होता है, लेकिन यहां गणना को आसान बनाने के लिए इसे गोल किया जाता है।

चरण 5. इस संख्या को पिछली संख्या से गुणा करें।
कोण को 360 से विभाजित करने के बाद प्राप्त संख्या को त्रिज्या के वर्ग से pi को गुणा करने के बाद प्राप्त संख्या से गुणा करें। ऊपर के उदाहरण के लिए, परिणाम 102, 214 (गोल करने के बाद) है।
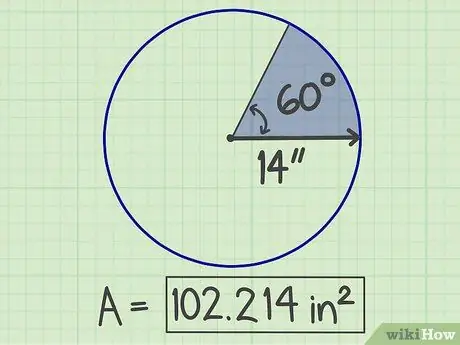
चरण 6. परिणाम लिखें।
प्राप्त संख्या सेक्टर का क्षेत्रफल है, जो 102, 214 वर्ग इंच है।
विधि ५ का ७: दीर्घवृत्त
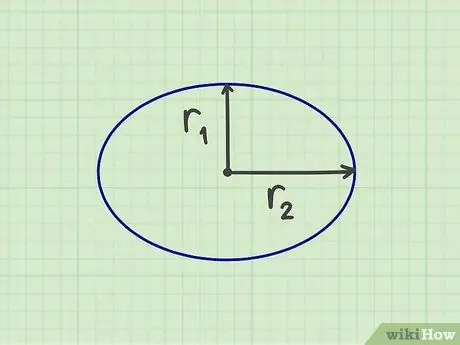
चरण 1. आवश्यक संख्या को मापें।
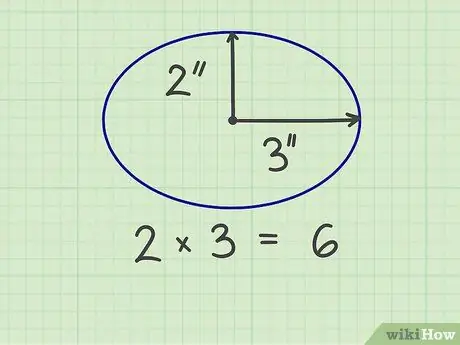
एक दीर्घवृत्त के क्षेत्रफल की गणना करने के लिए, आपको दो "त्रिज्या" मापने की आवश्यकता है, अर्थात् छोटी त्रिज्या और लंबी त्रिज्या, जो दीर्घवृत्त की आधी चौड़ाई और आधी ऊंचाई है। आप दीर्घवृत्त के केंद्र से सबसे छोटी भुजा तक की छोटी त्रिज्या और दीर्घवृत्त के केंद्र से सबसे लंबी भुजा तक की त्रिज्या को भी माप सकते हैं। छोटी त्रिज्या को लंबी त्रिज्या का समकोण बनाना चाहिए।
वास्तविक दुनिया में, आपको इसे स्वयं मापने की आवश्यकता हो सकती है, लेकिन जब गृहकार्य करने की बात आती है, तो शिक्षक आमतौर पर आकृति की तस्वीर के साथ संख्याएं लिख चुका होता है।
चरण 2. दो अंगुलियों को गुणा करें।
उदाहरण के लिए, एक दीर्घवृत्त 6 इंच चौड़ा और 4 इंच ऊँचा होता है, इसलिए त्रिज्याएँ 3 इंच और 2 इंच होती हैं। जब दो संख्याओं को गुणा किया जाता है, तो परिणाम 6 (3 x 2) होता है।

चरण 3. परिणाम को pi से गुणा करें।
पाई (π) विभिन्न सूत्रों में प्रयुक्त एक महत्वपूर्ण संख्या है। यदि आप कैलकुलेटर का उपयोग कर रहे हैं, तो वास्तव में सटीक परिणाम प्राप्त करने के लिए पाई कुंजी दबाएं। अन्यथा, अपनी गणना को आसान बनाने के लिए, आप अल्पविराम के बाद pi को कुछ अंकों में गोल कर सकते हैं, उदाहरण के लिए, 3, 14159। जब आप इस संख्या को त्रिज्या के वर्ग से गुणा करते हैं, तो परिणाम 18,84954 होता है।
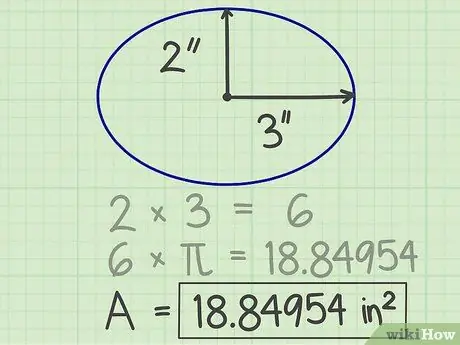
चरण 4. परिणाम लिखिए।
उपरोक्त गणना से प्राप्त संख्या दीर्घवृत्त का क्षेत्रफल है। ऊपर के उदाहरण में, दीर्घवृत्त का क्षेत्रफल 18.84954 वर्ग इंच है।
विधि ६ का ७: त्रिभुज
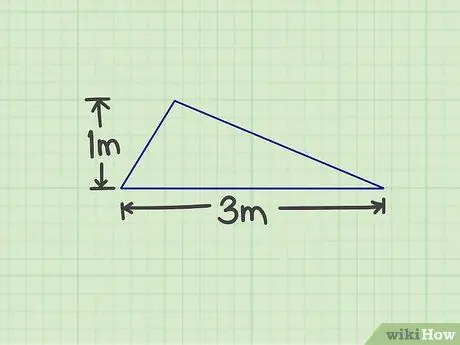
चरण 1. आवश्यक संख्या को मापें।
आपको त्रिभुज के आधार और ऊंचाई को मापने की आवश्यकता है। त्रिभुज की कोई भी भुजा आधार हो सकती है, जब तक आप ऊँचाई माप सकते हैं। उदाहरण के लिए, एक त्रिभुज है जिसका आधार 3 मीटर और ऊंचाई 1 मीटर है।
वास्तविक दुनिया में, आपको इसे स्वयं मापने की आवश्यकता हो सकती है, लेकिन जब गृहकार्य करने की बात आती है, तो शिक्षक आमतौर पर आकृति की तस्वीर के साथ संख्याएं लिख चुका होता है।
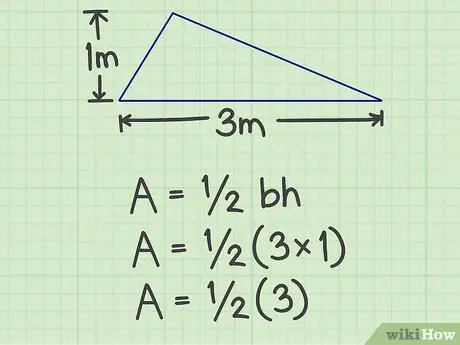
चरण 2. आधार को ऊंचाई से गुणा करें।
ऊपर के उदाहरण के लिए, परिणाम 3 (3x1) है।
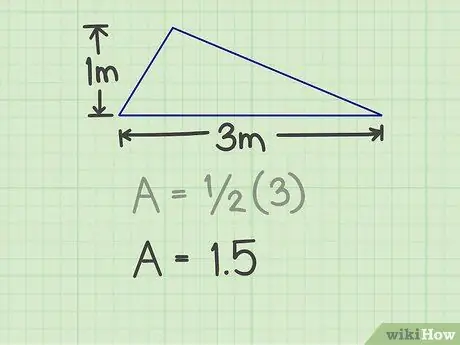
चरण 3. परिणाम को 1/2 से गुणा करें।
यह गुणन संख्या 1, 5 उत्पन्न करेगा।
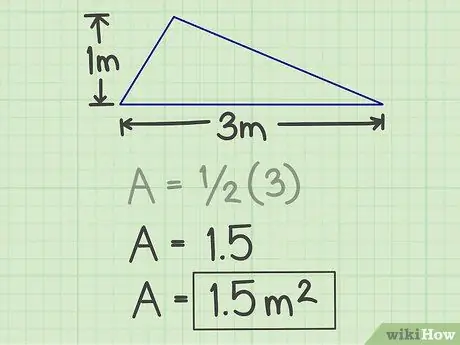
चरण 4. परिणाम लिखिए।
उपरोक्त गणना से उत्पन्न संख्या त्रिभुज का क्षेत्रफल है, और ऊपर के उदाहरण से इसका क्षेत्रफल 1.5 वर्ग मीटर है।
विधि 7 का 7: कॉम्प्लेक्स फ्लैट बिल्ड
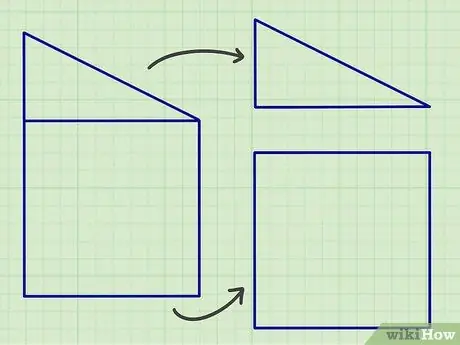
चरण 1. ऊपर दी गई मानक ज्यामितीय आकृतियों वाले भागों में जटिल समतल आकृतियों को अलग करें।
यदि आप जो कर रहे हैं वह गृहकार्य है, तो जटिल आकार को पहले चर्चा की गई सपाट आकृतियों में विभाजित करना आसान हो सकता है, लेकिन वास्तविक दुनिया में, सटीक गणना परिणाम प्राप्त करने के लिए आपको सपाट आकार को बहुत सारे सपाट आकार में विभाजित करने की आवश्यकता हो सकती है.
शुरू करने का एक अच्छा तरीका उन रेखाओं की तलाश करना है जो समानांतर हैं या जो एक निश्चित कोण बनाती हैं, क्योंकि अधिकांश सपाट आकार इन आकृतियों से बने होते हैं।
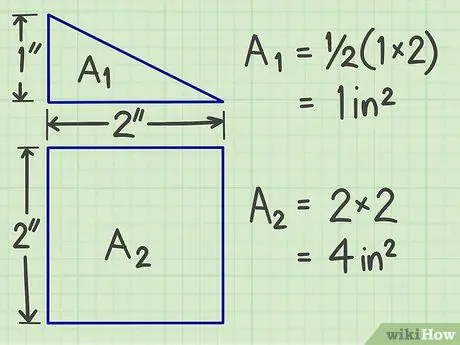
चरण 2. पृथक्करण के परिणामस्वरूप प्रत्येक समतल आकृतियों के क्षेत्रफल की गणना कीजिए।
प्रत्येक समतल आकृति का क्षेत्रफल ज्ञात करने के लिए उपरोक्त विधियों का प्रयोग करें।
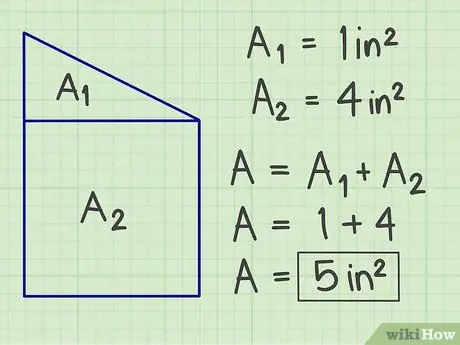
चरण 3. परिणाम जोड़ें।
अपने जटिल समतल आकृति का कुल क्षेत्रफल प्राप्त करने के लिए सभी परिकलित क्षेत्रों को जोड़ें।
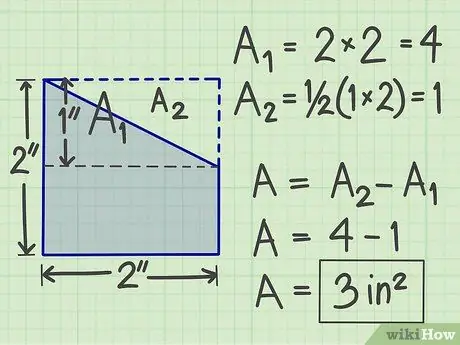
चरण 4. दूसरी विधि का प्रयोग करें।
जटिल फ्लैट आकार के आकार के आधार पर आप कई अन्य तरीकों को आजमा सकते हैं। उदाहरण के लिए, आप इसमें एक काल्पनिक समतल आकार भी जोड़ सकते हैं ताकि यह एक मानक ज्यामितीय समतल आकार बन जाए। उसके बाद क्षेत्रफल की गणना करें, फिर उस काल्पनिक सपाट आकार के क्षेत्रफल को घटाएं जिसे आप जोड़ते थे।
टिप्स
- यदि आपको गणित की गणनाओं को हल करने में सहायता चाहिए तो इस कैलकुलेटर का उपयोग करें।
- अगर आपको अभी भी परेशानी हो रही है तो किसी मित्र से मदद मांगें!
चेतावनी
- यह सुनिश्चित करने के लिए कि वे सही हैं, गणना परिणामों को दोबारा जांचना हमेशा बेहतर होता है!
- सुनिश्चित करें कि गणना करते समय आपके द्वारा उपयोग की जाने वाली इकाइयाँ सभी समान (सेमी, मी, इंच, आदि) हैं, इसलिए मिश्रित इकाइयों के कारण आप गलत गणना नहीं करते हैं!







