गति की गणना करने के 3 तरीके

2024 लेखक: Jason Gerald | [email protected]. अंतिम बार संशोधित: 2024-01-16 19:30

गति एक गणना है कि एक समय में कोई चीज कितनी तेजी से आगे बढ़ रही है। यदि आपने कभी चलती कार के स्पीडोमीटर को देखा है, तो आप गति की गणना देखेंगे - सुई जितनी दूर जाएगी, वाहन की गति उतनी ही अधिक होगी। आपके पास किस प्रकार की जानकारी है, इसके आधार पर गति की गणना करने के कई तरीके हैं। सामान्य तौर पर, सूत्र गति = दूरी/समय (या k = j/w) गति की गणना करने का सबसे आसान तरीका है।

कदम

विधि 1 में से 3: मानक गति गणना फ़ार्मुलों का उपयोग करना

चरण 1. किसी वस्तु द्वारा तय की गई दूरी ज्ञात कीजिए।

किसी चीज़ की गति ज्ञात करने के लिए अधिकांश लोग जिस मूल सूत्र का उपयोग करते हैं, उसका उपयोग करना बहुत आसान है। सबसे पहले, आपको यह जानना होगा कि "मापी गई वस्तु ने कितनी दूरी तय की है"। दूसरे शब्दों में, वस्तु के प्रारंभिक बिंदु और अंत बिंदु के बीच की दूरी क्या है?

इस फॉर्मूले को एक उदाहरण से समझना आसान है। मान लीजिए कि हम "161 किलोमीटर" के लिए कार से खेल के मैदान में यात्रा करते हैं। कुछ चरणों में, हम इस जानकारी का उपयोग सूत्र की गणना को पूरा करने के लिए कर सकते हैं।

चरण 2. उस दूरी को तय करने में वस्तु को लगने वाला समय ज्ञात कीजिए।

अगली जानकारी जो आपको चाहिए वह यह है कि वस्तु को एक निश्चित दूरी तक पहुँचने में कितना समय लगता है। दूसरे शब्दों में, वस्तु को प्रारंभ बिंदु से अंत बिंदु तक जाने में कितना समय लगता है?

इस उदाहरण में, मान लें कि वस्तु लगभग लेती है। दो घंटे गंतव्य तक पहुंचने के लिए।

चरण 3. दूरी को वस्तु का वेग ज्ञात करने में लगने वाले समय से भाग दें।

वस्तु की गति जानने के लिए आपको केवल इन दो सूचनाओं की आवश्यकता है। समय की दूरी वस्तु के वेग के बराबर होती है।

इस उदाहरण में, 161 किलोमीटर/2 घंटे = 80.5 किलोमीटर/घंटा.

चरण 4. प्रयुक्त इकाई को न भूलें।

अपने उत्तर में सही इकाइयों का उपयोग करना बहुत महत्वपूर्ण है (जैसे किलोमीटर प्रति घंटा, आदि) इन इकाइयों के बिना, लोगों के लिए आपके उत्तर का अर्थ समझना बहुत कठिन है। यदि आप स्कूल से असाइनमेंट करते समय गलत यूनिट का उपयोग करते हैं तो आप अंक खो सकते हैं।

गति की इकाई है समय की इकाई से दूरी की इकाई. उदाहरण के लिए, चूँकि हम दूरी को किलोमीटर में और समय को घंटों में मापते हैं, इसलिए उपयोग की जाने वाली इकाइयाँ हैं किलोमीटर/घंटा (या किलोमीटर प्रति घंटा).

विधि 2 का 3: अधिक कठिन गणनाओं को हल करना

चरण 1. दूरी और समय की समस्या को हल करने के लिए कई अलग-अलग चर खोजें।

एक बार जब आप गति के मूल सूत्र को समझ लेते हैं, तो आप गति के अलावा अन्य गणना करने के लिए इसका उपयोग कर सकते हैं। उदाहरण के लिए, यदि पहले आप केवल वस्तु के वेग और एक अन्य चर को जानते हैं, तो आप अज्ञात जानकारी को खोजने के लिए उपरोक्त सूत्र को पुनर्व्यवस्थित कर सकते हैं।

• उदाहरण के लिए, मान लीजिए कि हम जानते हैं कि एक ट्रेन चार घंटे में 20 किलोमीटर प्रति घंटे की रफ्तार से चलती है, लेकिन हम यह नहीं जानते कि उसने कितनी दूर की यात्रा की है। यह पता लगाने के लिए, हम सूत्र को निम्नलिखित तरीके से पुनर्व्यवस्थित कर सकते हैं:

  गति = दूरी/समय

  गति × समय = (दूरी/समय) × समय

  गति × समय = दूरी

  20 किमी/घंटा × 4 घंटे = दूरी = 80 किलोमीटर

चरण २। आपके द्वारा उपयोग की जाने वाली इकाइयों को आवश्यकतानुसार रूपांतरित करें।

कभी-कभी, आप एक निश्चित इकाई का उपयोग करके गति की गणना कर सकते हैं, लेकिन इसे दूसरी इकाई में बदलने की आवश्यकता होती है। इस मामले में, आपको सही इकाइयों के अनुसार उत्तर प्राप्त करने के लिए रूपांतरण कारक का उपयोग करने की आवश्यकता है। ऐसा करने के लिए, बस इकाइयों के बीच संबंध को भिन्न रूप में लिखें और गुणा करें। गुणा करते समय, अवांछित इकाइयों को हटाने के लिए आवश्यक अंश को उलट दें। यह तरीका जितना लगता है उससे कहीं ज्यादा आसान है!

• उदाहरण के लिए, मान लें कि उपरोक्त उदाहरण समस्या में, हमें किलोमीटर के बजाय मीलों में उत्तर चाहिए। एक मील लगभग 1.6 किलोमीटर के बराबर होता है। तो, हम रूपांतरण इस प्रकार कर सकते हैं:

  80 किलोमीटर × 1 मील/1.6 किलोमीटर = ५० मील

• याद रखें, क्योंकि अंश के नीचे किलोमीटर दिखाई देता है, यह पिछले उत्तर से किलोमीटर को हटा देता है, इसलिए अंतिम परिणाम मील का उपयोग करता है।
• यह वेबसाइट आमतौर पर उपयोग की जाने वाली अधिकांश इकाइयों के लिए रूपांतरण सुविधाएँ प्रदान करती है।

चरण 3. "दूरी" चर को आवश्यकतानुसार दूरी सूत्र से बदलें।

वस्तुएँ हमेशा सीधे, चिकने पथ में नहीं चलती हैं। यदि यह सत्य है, तो आप मानक वेग सूत्र में दूरी की एक इकाई के रूप में केवल एक संख्यात्मक मान दर्ज करने में सक्षम नहीं हो सकते हैं। हालांकि, आपको सूत्र k = j/w के अक्षर j को किसी ऐसे सूत्र से बदलना पड़ सकता है जो वस्तु द्वारा तय की गई दूरी से मिलता-जुलता हो।

• उदाहरण के लिए, मान लीजिए कि एक हवाई जहाज हवा में 5 बार 20 मील की दूरी तय करता है। विमान ने आधे घंटे में चक्कर पूरा किया। इस उदाहरण में, हमें अभी भी विमान द्वारा तय की गई कुल दूरी का पता लगाना होगा, इससे पहले कि हम इसकी गति निर्धारित कर सकें। हम इस सूत्र में j के बजाय वृत्त के चारों ओर की दूरी (इसके चारों ओर की दूरी) की गणना के लिए सूत्र का उपयोग कर सकते हैं। यह सूत्र परिधि = 2πr है जहाँ r = वृत्त की त्रिज्या है। इसे हल करने का तरीका यहां बताया गया है:

  के = (2 × × आर)/डब्ल्यू

  के = (2 × × 10)/0.5

  कश्मीर = 62.83/0.5 = 125.66 मील/घंटा

चरण 4. समझें कि k = j/w औसत वेग देता है।

वेग ज्ञात करने के लिए हम जिस आसान और सरल सूत्र का उपयोग करते हैं, उसमें एक खामी है। परिणामी मूल्य तकनीकी रूप से औसत गति है। इसका मतलब यह है कि सूत्र मानता है कि जिस वस्तु को आप माप रहे हैं वह उसी वेग का उपयोग करती है जैसे वह चलती है। जैसा कि हम नीचे देखेंगे, एक क्षण में किसी वस्तु का वेग ज्ञात करना कहीं अधिक कठिन होगा।

इस अंतर को स्पष्ट करने के लिए, कल्पना कीजिए कि आपने पिछली बार कार से कब यात्रा की थी। यह संभावना नहीं है कि आप उसी गति से यात्रा कर रहे होंगे जैसे आप यात्रा कर रहे हैं। हालांकि, आप आमतौर पर अपनी यात्रा कम गति से शुरू करेंगे और रास्ते में धीरे-धीरे अपनी गति बढ़ाते जाएंगे, लाल बत्ती, ट्रैफिक जाम आदि के कारण रुकेंगे। यदि आप यात्रा के दौरान गति ज्ञात करने के लिए मानक गति सूत्र का उपयोग करते हैं, तो उस गति में परिवर्तन का पता नहीं लगाया जा सकता है। हालांकि, आपको एक उत्तर मिलेगा जो आपके द्वारा यात्रा किए जाने वाले सभी गति अंतरों की औसत गति को दर्शाता है।

विधि 3 में से 3: त्वरित गति की गणना

ध्यान दें:

यह खंड उन तकनीकों का उपयोग करता है जो उन लोगों से कम परिचित हैं जिन्होंने कभी पथरी का अध्ययन नहीं किया है। सहायता के लिए कलन पर हमारे लेख पढ़ें।

चरण 1. समझें कि वेग को त्वरण की दर के रूप में परिभाषित किया गया है।

उच्च-स्तरीय वेग गणना काफी भ्रमित करने वाली है क्योंकि गणितज्ञ और वैज्ञानिक "गति" और "त्वरण" का वर्णन करने के लिए विभिन्न परिभाषाओं का उपयोग करते हैं। त्वरण के दो घटक हैं: एक "दर" और एक "दिशा"। दर वस्तु की गति के बराबर है। दिशा में परिवर्तन से त्वरण में परिवर्तन होगा, लेकिन वेग में परिवर्तन नहीं होगा।

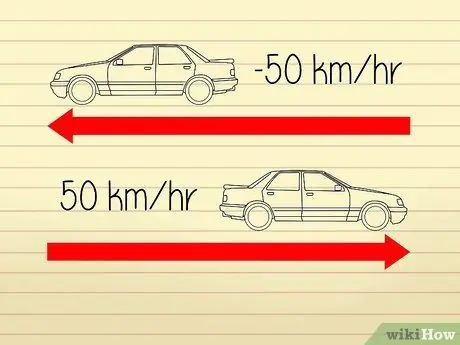
• उदाहरण के लिए, मान लीजिए कि दो कारें विपरीत दिशाओं में चल रही हैं। दोनों कारों के स्पीडोमीटर 50 किमी/घंटा का आंकड़ा प्रदर्शित करते हैं, इसलिए वे दोनों एक ही गति से यात्रा कर रहे हैं। हालांकि, चूंकि कारें एक-दूसरे से दूर जा रही हैं, हम कह सकते हैं कि कारों में से एक का "त्वरण" -50 किमी/घंटा है जबकि दूसरे में 50 किमी/घंटा का "त्वरण" है।
• तात्कालिक वेग गणनाओं की तरह, आप तात्कालिक त्वरण गणना भी कर सकते हैं।

चरण 2. ऋणात्मक त्वरण को मापने के लिए निरपेक्ष मानों का उपयोग करें।

एक वस्तु में त्वरण की ऋणात्मक दर हो सकती है (यदि वह किसी अन्य वस्तु के सापेक्ष ऋणात्मक दिशा में गति कर रही है)। हालांकि, कोई नकारात्मक गति नहीं है। तो, इस मामले में, दर का निरपेक्ष मान वस्तु के वेग को इंगित करता है।

इस कारण से, उपरोक्त उदाहरण समस्या में, दोनों कारों की गति है 50 किमी/घंटा.

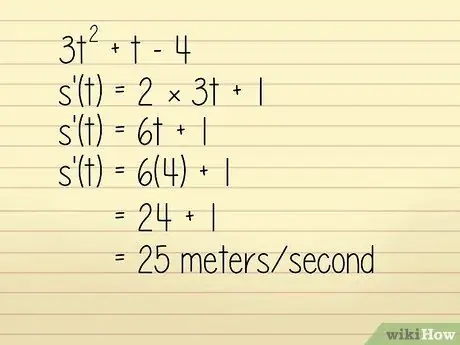
चरण 3. फलन की स्थिति का अवकलज लीजिए।

यदि आपके पास एक फ़ंक्शन k(w) है जो समय की गणना किए बिना किसी वस्तु की स्थिति दिखाता है, तो k(w) का व्युत्पन्न समय की आवश्यकता के बिना त्वरण दिखाएगा। बस इस फॉर्मूले में टाइम वैल्यू को प्लग करें ताकि वेरिएबल w (या जो भी टाइम वैल्यू इस्तेमाल किया गया हो) उस समय के हिसाब से तेज हो जाए। यहां से आप आसानी से वस्तु का वेग ज्ञात कर सकते हैं।

• उदाहरण के लिए, मान लीजिए कि एक मीटर में किसी वस्तु की स्थिति समीकरण 3q. में वर्णित है² + डब्ल्यू - 4 जहां डब्ल्यू = सेकंड में समय। हम वस्तु का वेग w = 4 सेकंड पर जानना चाहते हैं। इस मामले में, आप इसे हल कर सकते हैं:

  3w² +डब्ल्यू - 4

  k'(w) = 2 × 3w + 1

  के'(डब्ल्यू) = 6w + 1

• अब, हम w = 4 दर्ज करते हैं:

  के'(डब्ल्यू) = 6(4) + 1 = 24 + 1 = 25 मीटर/सेकंड. तकनीकी रूप से यह त्वरण की गणना है, लेकिन चूंकि यह सकारात्मक है और प्रश्न में दिशा का उल्लेख नहीं किया गया है, हम इसका उपयोग वेग खोजने के लिए कर सकते हैं।

चरण 4. समाकलन त्वरण फलन लें।

त्वरण समय के साथ किसी वस्तु के त्वरण में परिवर्तन को मापने का एक तरीका है। इस लेख में पूरी तरह से समझाया जाने के लिए यह विषय बहुत जटिल है। हालांकि, यह ध्यान रखना उपयोगी है कि जब आपके पास एक फ़ंक्शन a(w) होता है जो समय के संबंध में त्वरण का प्रतिनिधित्व करता है, तो a(w) का इंटीग्रल उस समय के आधार पर त्वरण का परिणाम लौटाएगा। याद रखें, किसी वस्तु के प्रारंभिक त्वरण को जानना बहुत उपयोगी है ताकि आप उस परिणाम के स्थिरांक को अनंत समाकलन से परिभाषित कर सकें।

• उदाहरण के लिए, मान लें कि किसी वस्तु का त्वरण स्थिर है (m/s. में)² a(w) = -30 के परिणामस्वरूप। यह भी कहें कि वस्तु का प्रारंभिक त्वरण 10 m/s है। हमें w = 12 सेकंड पर वेग ज्ञात करने की आवश्यकता है। इस मामले में, हम इसे हल कर सकते हैं:

  ए (डब्ल्यू) = -30

  p(w)= a(w)dw = -30dw = -30w + C

• C को खोजने के लिए, हम p(w) को w = 0 के लिए हल करेंगे। याद रखें कि वस्तु का प्रारंभिक त्वरण 10 m/s है।

  पी(0) = 10 = -30(0) + सी

  10 = सी, तो पी(डब्ल्यू) = -30w + 10

• अब, हम w = 12 सेकंड दर्ज कर सकते हैं।

  पी(१२) = -30(१२) + १० = -३६० + १० = -३५०। चूँकि वेग त्वरण का निरपेक्ष मान है, वस्तु का वेग है 350 मीटर/सेकंड.

टिप्स

• अभ्यास महान बनाता है! उपरोक्त उदाहरण समस्या में संख्याओं को बदलकर अपना प्रश्न स्वयं बनाने का प्रयास करें।
• यदि आप बेहतर गणना गति के लिए कैलकुलस का अभ्यास करने का एक त्वरित तरीका ढूंढ रहे हैं, तो यहां ऑनलाइन डेरिवेटिव कैलकुलेटर और यहां ऑनलाइन इंटीग्रल कैलकुलेटर का उपयोग करें।