गणित कठिन है। जब आप कई अलग-अलग सिद्धांतों और विधियों को याद करने का प्रयास करते हैं तो बुनियादी अवधारणाओं को भूलना भी आसान होता है। यहाँ भिन्नों को सरल बनाने के दो नए तरीके दिए गए हैं।
कदम
विधि 1: 4 में से सबसे बड़ा सामान्य कारक का उपयोग करना

चरण 1. अंश और हर के गुणनखंड लिखिए।
गुणनखंड वे संख्याएँ हैं जिन्हें आप दूसरी संख्या प्राप्त करने के लिए गुणा कर सकते हैं। उदाहरण के लिए, ३ और ४ १२ के गुणनखंड हैं क्योंकि आप १२ प्राप्त करने के लिए उन्हें एक साथ गुणा कर सकते हैं। किसी संख्या के गुणनखंडों को लिखने के लिए, आपको बस उन सभी संख्याओं को लिखने की आवश्यकता है जिन्हें उस संख्या को प्राप्त करने के लिए गुणा किया जा सकता है, और विभाज्य हैं कारकों द्वारा।
-
कारक 1 को शामिल करना न भूलें, सबसे छोटी से सबसे बड़ी संख्या के गुणनखंड लिखिए। उदाहरण के लिए, यहां बताया गया है कि आप भिन्न 24/32 के अंश और हर को कैसे लिखते हैं:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

चरण 2. अंश और हर का सबसे बड़ा सामान्य गुणनखंड (GCF) ज्ञात कीजिए।
GCF सबसे बड़ी संख्या है जो दो या दो से अधिक संख्याओं को समान रूप से विभाजित कर सकती है। संख्या के सभी गुणनखंडों को लिख लेने के बाद, आपको बस इतना करना है कि वह सबसे बड़ी संख्या ज्ञात करें जो गुणनखंडों की दोनों सूचियों में समान हो।
-
24: 1, 2, 3, 4, 6,
चरण 8., 12, 24.
-
32: 1, 2, 4,
चरण 8., 16, 32.
-
24 और 32 का GCF 8 है क्योंकि 8 सबसे बड़ी संख्या है जो 24 और 32 को समान रूप से विभाजित कर सकती है।

चरण 3. अंश और भिन्न को GCF से भाग दें।
अब जबकि आपको GCF मिल गया है, आपको बस इतना करना है कि अंश और हर को उस संख्या से भाग दें ताकि आपके भिन्न को उसके सरलतम रूप में सरल बनाया जा सके। यहाँ यह कैसे करना है:
- 24/8 = 3
- 32/8 = 4
- साधारण अंश 3/4 है।

चरण 4. अपने काम की जाँच करें।
यदि आप यह सुनिश्चित करना चाहते हैं कि आपने भिन्न को सही ढंग से सरलीकृत किया है, तो आपको मूल भिन्न को वापस पाने के लिए नए अंश और हर को उनके GCF से गुणा करना होगा। यहाँ यह कैसे करना है:
- 3 * 8 = 24
- 4 * 8 = 32
-
आप अपने मूल स्वरूप में वापस आ गए हैं, जो 24/32 है।
आप यह सुनिश्चित करने के लिए भिन्न की जांच भी कर सकते हैं कि इसे और सरल नहीं बनाया जा सकता है। चूँकि 3 एक अभाज्य संख्या है, इसे केवल 1 और स्वयं से विभाजित किया जा सकता है, और चार 3 से विभाज्य नहीं है, इसलिए भिन्न को और सरल नहीं बनाया जा सकता है।
विधि २ का ४: छोटी संख्याओं से विभाजित करते रहें

चरण 1. एक छोटी संख्या चुनें।
इस पद्धति का उपयोग करते हुए, आपको केवल एक छोटी संख्या चुननी होगी, जैसे कि 2, 3, 4, 5 या 7, से शुरू करने के लिए। यह सुनिश्चित करने के लिए भिन्नों को देखें कि प्रत्येक भाग आपके द्वारा चुनी गई संख्या से विभाज्य है। उदाहरण के लिए, यदि आपके पास भिन्न 24/108 है, तो 5 को न चुनें क्योंकि वे 5 से विभाज्य नहीं हैं। हालाँकि, यदि आपके पास भिन्न 25/60 है, तो 5 उपयोग करने के लिए सही संख्या है।
भिन्न के लिए 24/32, 2 एक अच्छी संख्या है। चूँकि दोनों संख्याएँ सम संख्याएँ हैं, इसलिए वे 2 से विभाज्य हैं।

चरण 2. भिन्न के अंश और हर को संख्या से विभाजित करें।
नई भिन्न में एक नया अंश और हर होगा, जो आपको भिन्न के ऊपर और नीचे के अंश को 24/32 से 2 से विभाजित करने पर मिलता है। इसे करने का तरीका यहां बताया गया है:
- 24/2 = 12
- 32/2 = 16
- आपका नया अंश 12/16 है।
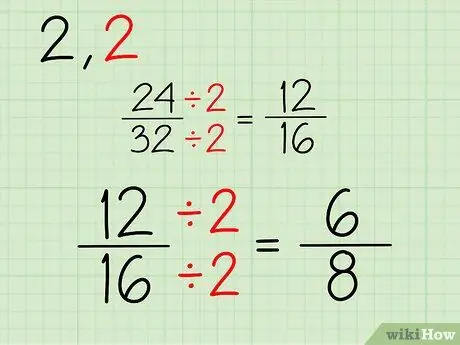
चरण 3. दोहराएँ।
इस प्रक्रिया को जारी रखें। चूँकि दोनों संख्याएँ सम संख्याएँ हैं, आप 2 से विभाजित करना जारी रख सकते हैं। यदि एक या दोनों अंश और हर विषम संख्याएँ हैं, तो आप दूसरी संख्या से विभाजित करने का प्रयास कर सकते हैं। यहाँ १२/१६ अंश को सरल बनाने की प्रक्रिया है:
- 12/2 = 6
- 16/2 = 8
- आपका नया अंश 6/8 है।

चरण 4. संख्या को तब तक विभाजित करते रहें जब तक कि वह विभाज्य न हो जाए।
नया अंश और हर भी सम संख्याएँ हैं, इसलिए आप 2 से भाग देना जारी रख सकते हैं। यहाँ यह कैसे करना है:
- 6/2 = 3
- 8/2 = 4
- आपका नया अंश 3/4 है।

चरण 5. सुनिश्चित करें कि भिन्न को और सरल नहीं किया जा सकता है।
भिन्न में ३/४, ३ एक अभाज्य संख्या है, इसलिए गुणनखंड केवल १ और स्वयं हैं, और ४, ३ से विभाज्य नहीं है, इसलिए भिन्न को और सरल नहीं किया जा सकता है। यदि भिन्न के अंश या हर को आपके द्वारा चुनी गई संख्या से विभाजित नहीं किया जा सकता है, तब भी आप इसे किसी अन्य संख्या से विभाजित करने में सक्षम हो सकते हैं।
उदाहरण के लिए, यदि आपके पास अंश 10/40 है, और आप अंश और हर को 5 से विभाजित करते हैं, तो परिणाम 2/8 होता है। आप अंश और भिन्न को 5 से विभाजित नहीं कर सकते हैं, लेकिन आप दोनों को 2 से विभाजित कर सकते हैं ताकि अंतिम परिणाम 1/4 हो।

चरण 6. अपने काम की जाँच करें।
यह सुनिश्चित करने के लिए कि आपको प्रारंभिक भिन्न प्राप्त हो, 3/4 को 2/2 से तीन बार गुणा करें, जो कि 24/32 है। यहाँ यह कैसे करना है:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- ध्यान दें कि आप 24/32 को 2 * 2 * 2 से विभाजित कर रहे हैं, जो कि 8 से विभाजित करने के समान है, जो 24 और 32 का सबसे बड़ा GCF है।
विधि ३ का ४: कारकों को लिखना

चरण 1. अपना अंश लिखिए।
अपने पेपर के दाहिनी ओर एक बड़ी जगह छोड़ दें - आपको कारकों को लिखने के लिए इसकी आवश्यकता होगी।

चरण 2. अंश और हर के गुणनखंड लिखिए।
अकेले दोनों के कारक। कारकों को एक दूसरे के ऊपर लिखा जाना सबसे आसान तरीका है। नंबर 1 से शुरू करें और कारकों को लिखें।
-
उदाहरण के लिए, यदि आपका अंश 24/60 है, तो 24 से शुरू करें।
लिखें: २४ - १, २, ३, ४, ६, ८, १२, २४
-
फिर, संख्या 60।
लिखें: ६० - १, २, ३, ४, ५, ६, १०, १२, १५, २०, ३०, ६०

चरण 3. सबसे बड़े सामान्य कारक को खोजें और विभाजित करें।
यह शब्द आपकी मुद्रित पुस्तक में GCF के रूप में लिखा जा सकता है। अंश और हर को विभाजित करने वाली सबसे बड़ी संख्या क्या है? संख्या जो भी हो, दोनों संख्याओं को उस संख्या से भाग दें।
हमारे उदाहरण के लिए, सबसे बड़ी संख्या जो दोनों संख्याओं का गुणनखंड है, 12 है। इस प्रकार, हम 24 को 12 से और 60 को 12 से विभाजित करते हैं, जिससे हमें 2/5 मिलता है - हमारा साधारण अंश
विधि 4 का 4: प्राइम फैक्टर ट्री का उपयोग करना

चरण 1. अंश और हर के अभाज्य गुणनखंड ज्ञात कीजिए।
एक अभाज्य संख्या एक संख्या है जिसे किसी अन्य संख्या से विभाजित नहीं किया जा सकता है (स्वयं और 1 के अलावा, निश्चित रूप से)। 2, 3, 5, 7, और 11 अभाज्य संख्याओं के उदाहरण हैं।
- अंकगणित से शुरू करें। २४ से, २ और १२ में विभाजित करें। चूँकि २ पहले से ही एक अभाज्य संख्या है, आपको इसे अब और विभाजित करने की आवश्यकता नहीं है! फिर 12 को 2 संख्याओं में तोड़ें: 2 और 6. 2 अभाज्य संख्याएँ हैं - बढ़िया! अब 6 को 2 संख्याओं में विभाजित करें: 2 और 3। अब आपके पास 2, 2, 2 और 3 अभाज्य संख्याएँ हैं।
- अब हर पर काम करें। ६० से, अपने पेड़ को २ और ३० में विभाजित करें। ३० फिर २ और १५ में विभाजित करें। फिर १५ को ३ और ५ में विभाजित करें, जो दोनों अभाज्य संख्याएँ हैं। अब आपके पास 2, 2, 3 और 5 अभाज्य संख्याएँ हैं।
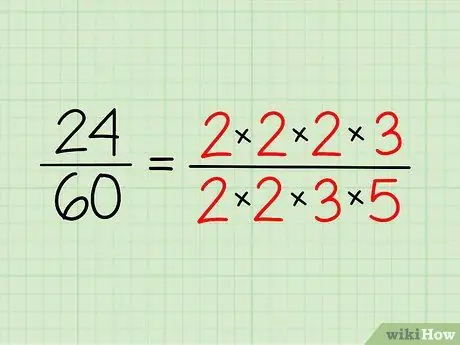
चरण 2. प्रत्येक संख्या का अभाज्य गुणनखंड लिखिए।
प्रत्येक संख्या के लिए आपके पास अभाज्य संख्याएँ लिखिए और उन्हें गुणन के रूप में लिखिए। आपको इसे गुणा करने की आवश्यकता नहीं है - यह देखना आसान बनाने का एक तरीका है।
- तो, 24 के लिए, आपके पास 2 x 2 x 2 x 3 = 24 है।
- 60 के लिए, आपके पास 2 x 2 x 3 x 5 = 60. है

चरण 3. समान कारकों को हटा दें।
कोई भी संख्या जो दोनों संख्याओं का भाग हो, त्यागी जा सकती है। इस उदाहरण में, समान गुणनखंड 2s और एक 3 का युग्म हैं। अलविदा!
- बाकी 2 और 5 - या 2/5 हैं! वही जवाब हमें ऊपर वाला रास्ता मिला।
- यदि भिन्न का अंश और हर सम संख्याएँ हैं, तो केवल दो से विभाजित न करें। तब तक भाग करना जारी रखें जब तक आपको प्राप्त संख्या को फिर से विभाजित न किया जा सके।







