क्रॉस गुणन दो समान अंशों के चर वाले समीकरणों को हल करने का एक तरीका है। एक चर अज्ञात मात्रा में संख्याओं के लिए एक प्लेसहोल्डर है और क्रॉस गुणन इसे एक साधारण समीकरण में बदल देता है, जिससे आप प्रश्न में चर का मान ज्ञात कर सकते हैं। जब आप किसी तुलना को पूरा करना चाहते हैं तो क्रॉस गुणा बहुत उपयोगी होता है। यहाँ यह कैसे करना है:
कदम
विधि 1 में से 2: एक चर का क्रॉस उत्पाद
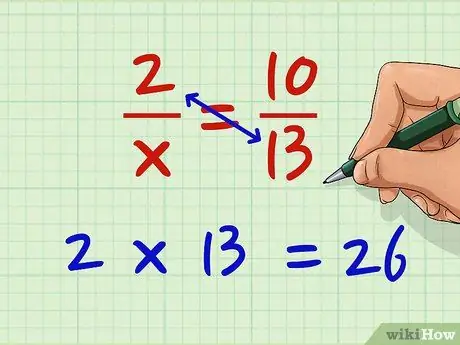
चरण 1. बाएँ हाथ के अंश के अंश को दाएँ हाथ के अंश के हर से गुणा करें।
मान लें कि आप समीकरण 2/x = 10/13 को हल करना चाहते हैं। अब, 2 को 13.2 x 13 = 26 से गुणा करें।
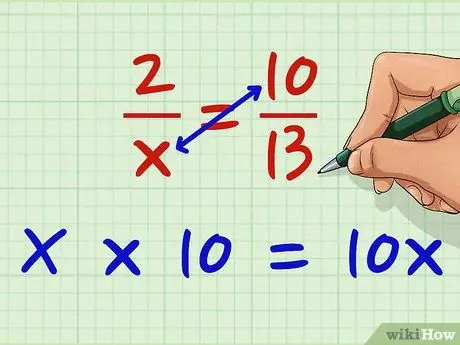
चरण 2. दाएँ हाथ के हर को बाएँ हाथ के हर से गुणा करें।
x को 10 से गुणा करें। X * 10 = 10x। आप पहले इस खंड को पार कर सकते हैं; इससे कोई फर्क नहीं पड़ता जब तक आप दोनों अंशों को दोनों हरों से तिरछे गुणा करते हैं।
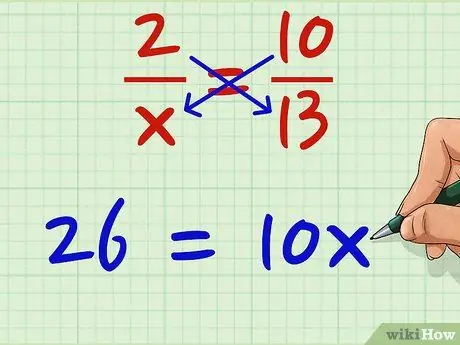
चरण 3. दोनों उत्पादों को समान बनाएं।
26 10x के बराबर है। 26 = 10x। इससे कोई फर्क नहीं पड़ता कि कौन दाएं या बाएं है; समान होने के कारण, आप उनका स्थान तब तक बदल सकते हैं जब तक आप उन सभी को एक साथ ले जाते हैं।
इसलिए यदि आप 2/x = 10/13, 2 * 13 = x * 10 या 26 = 10x का x मान ज्ञात करने का प्रयास करते हैं।

चरण 4. चर का मान ज्ञात कीजिए।
अब जब आपके पास 26 = 10x है, तो आप एक सामान्य अंश खोजने की कोशिश कर सकते हैं और 26 और 10 को उसी संख्या से विभाजित कर सकते हैं जो दोनों को विभाजित करती है। चूँकि दोनों सम संख्याएँ हैं, आप 2 से भाग दे सकते हैं; 26/2 = 13 और 10/2 = 5. शेषफल 13 = 5x है। अब, अकेले x लेते हुए, समीकरण के दोनों पक्षों को 5 से विभाजित करें। इसलिए 13/5 = 5/5 या 13/5 = x। यदि आप दशमलव रूप में उत्तर चाहते हैं, तो आप समीकरण के दोनों पक्षों को 10 से विभाजित करके 26/10 = 10/10 या 2,6 = x प्राप्त करने के लिए प्रारंभ कर सकते हैं।
विधि २ का २: बहुचर क्रॉस गुणन
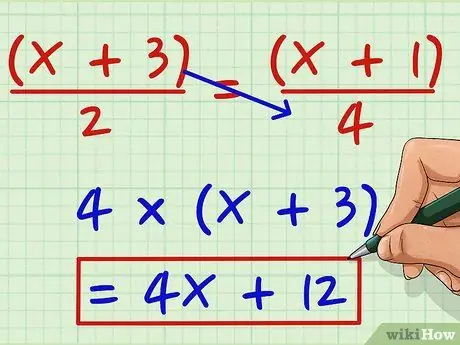
चरण 1. बाईं ओर के अंश को हर से दाईं ओर गुणा करें।
मान लें कि आप निम्नलिखित समीकरण को हल करना चाहते हैं: (x + 3)/2 = (x + 1)/4 । 4(x + 3) प्राप्त करने के लिए (x + 3) को 4 से गुणा करें। 4x + 12 प्राप्त करने के लिए 4 से गुणा करें।

चरण 2. दाईं ओर के अंश को बाईं ओर के हर से गुणा करें।
दूसरी तरफ प्रक्रिया को दोहराएं। (x+1) x 2 = 2(x+1) । 2x + 2 प्राप्त करने के लिए 2 से गुणा करें।

चरण 3. दोनों के गुणनफल को समान बनाएं और समान चरों को मिलाएं।
अब, परिणाम 4x + 12 = 2x + 2 है। समीकरण के दूसरी ओर चर x और अचर को मिलाइए।
- तो, दोनों पक्षों से 2x घटाकर 4x और 2x को मिलाएं। 2x में से 2x घटाने पर 0 शेष बचेगा। बाईं ओर, 4x - 2x = 2x, इसलिए शेष 2x है।
- अब, 12 और 2 को दोनों पक्षों से 12 घटाकर जोड़ दें। बाईं ओर 12 में से 12 घटाएं और परिणाम 0 है, फिर दाईं ओर 2 में से 12 घटाएं ताकि परिणाम 2 - 12 = -10 हो।
- शेषफल 2x = -10 है।

चरण 4. समाप्त करें।
आपको केवल समीकरण के दोनों पक्षों को 2 से विभाजित करना है। 2x/2 = -10/2 = x = -5। क्रॉस गुणा करने के बाद, आप पाते हैं कि x = -5। आप वापस जा सकते हैं और x का मान दर्ज करके अपने काम की जांच कर सकते हैं, जो कि -5 है, यह सुनिश्चित करने के लिए कि दोनों पक्ष समान हैं। यह समकक्ष निकला। यदि आप -5 को मूल समीकरण में जोड़ते हैं, तो परिणाम -1 = -1 होता है।
टिप्स
- ध्यान दें कि यदि आप एक ही समीकरण में अलग-अलग संख्याओं (5 कहते हैं) को जोड़ते हैं, तो परिणाम 2/5 = 10/13 होता है। यदि आप बाईं ओर को 5/5 से गुणा करते हैं, तो भी आपको 10/25 = 10/13 मिलता है, जो स्पष्ट रूप से गलत है। यह मामला इंगित करता है कि आपने क्रॉस गुणा त्रुटि की है।
- आप अपने परिणाम को मूल समीकरण में जोड़कर अपने उत्तर की जांच कर सकते हैं। यदि समीकरण एक सत्य कथन है, उदाहरण के लिए 1 = 1, तो आपका उत्तर सही है। यदि समीकरण एक गलत कथन बन जाता है, उदाहरण के लिए 0 = 1, आपने एक गलती की है। उदाहरण के लिए, 2/(2, 6) = 10/13 के लिए समीकरण में 2, 6 डालें। 10/13 = 10/13 प्राप्त करने के लिए बाईं ओर को 5/5 से गुणा करें। परिणाम एक सही कथन है, जो सरल होने पर 1 = 1 हो जाता है, इसलिए 2, 6 सही उत्तर है।







