यद्यपि सटीकता और सटीकता को अक्सर एक दूसरे के स्थान पर उपयोग किया जाता है, वे वास्तव में गणित और विज्ञान में बहुत अलग शब्द हैं। प्रेसिजन का मतलब है कि हर बार किए जाने पर माप का लगभग समान मूल्य होता है। उदाहरण के लिए, यदि आप लगातार 5 बार पैमाने पर कदम रखते हैं, तो एक पैमाना जिसमें अच्छी सटीकता होती है, हर बार समान द्रव्यमान दिखाएगा। गणित और विज्ञान में, सटीक गणना करना यह निर्धारित करने के लिए बहुत महत्वपूर्ण है कि आपके उपकरण और माप अच्छा डेटा प्राप्त करने के लिए ठीक से काम कर रहे हैं या नहीं। सौभाग्य से, सटीकता की गणना करना काफी आसान है।
कदम

चरण 1. सटीकता और सटीकता के बीच अंतर जानें।
सटीक मापता है कि आपके उपकरण कितनी अच्छी तरह काम करते हैं, न कि वे क्या मापते हैं। सटीकता जांचती है कि आपका उत्तर कितना सही है। उदाहरण के लिए, यदि आपका द्रव्यमान 9 किग्रा है और आपका पैमाना 8.7 किग्रा है, तो आपका पैमाना सटीक नहीं है। यदि आपका पैमाना आपके वजन के हर बार 8.7 किलोग्राम दिखाता है, तो यह अभी भी सटीक है, हालांकि सटीक नहीं है।
इन तीरंदाजी शब्दों में दो शब्दों के बारे में सोचें: शुद्धता अगर हम हर बार शूट करने पर तीरंदाजी लक्ष्य (बुल्सआई) के केंद्र सर्कल से टकराते हैं। शुद्धता अगर हम हर बार शूट करते समय एक ही स्थान पर हिट करते हैं, भले ही वह स्थान वह लक्ष्य न हो जिसे हम हिट करना चाहते हैं।

चरण 2. कई माप रिकॉर्ड करें।
सटीकता की गणना करने के लिए, आपको किसी चीज़ के बारे में डेटा चाहिए। उदाहरण के लिए, यदि आप अपने पैमाने की शुद्धता की जांच करना चाहते हैं, तो आप उस पर खड़े हो सकते हैं और पैमाने पर दिखाई गई संख्या को 15 बार रिकॉर्ड कर सकते हैं।
सटीकता की गणना करने के लिए आपको समान परिस्थितियों में एक ही वस्तु के कई मापों को रिकॉर्ड करना होगा। आप 10 अलग-अलग लोगों का वजन नहीं कर सकते और परिणामों की तुलना नहीं कर सकते।

चरण 3. अपने डेटा का माध्य या औसत ज्ञात करें।
सटीकता में बदलाव को नोटिस करने के लिए, आपको अपने डेटा की तुलना किसी चीज़ से करनी होगी। माध्य या औसत आपके डेटा का केंद्र बिंदु है और एक अच्छा बेंचमार्क है। माध्य ज्ञात करने के लिए, आपके द्वारा लिए गए सभी मापों को जोड़ें और संख्या को आपके द्वारा लिए गए मापों की संख्या से विभाजित करें। यदि, अपने द्रव्यमान का वजन करते समय, आपने द्रव्यमान दर्ज किया: 12 किग्रा, 11 किग्रा, 14 किग्रा, 13 किग्रा और 12 किग्रा, तो आपका माध्य होगा:
(12 किग्रा + 11 किग्रा + 14 किग्रा + 13 किग्रा + 12 किग्रा)/5 = 62/5 = 12.4 किग्रा
. दूसरे शब्दों में, दर्ज किया गया औसत द्रव्यमान है 12.4 किग्रा.
आप उन संख्याओं का भी उपयोग कर सकते हैं जिन्हें आप पहले से जानते हैं और माध्य का उपयोग करने की आवश्यकता नहीं है। उदाहरण के लिए, आप 10 किलो आलू के बैग का उपयोग कर सकते हैं और अपने आंकड़ों की तुलना इस संख्या से कर सकते हैं।
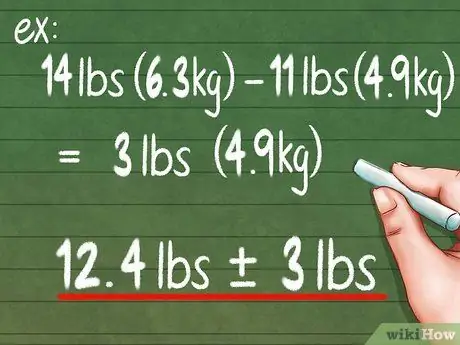
चरण 4. सरल सटीक गणना के लिए मानक श्रेणियों का उपयोग करें।
रेंज सटीकता निर्धारित करने का सबसे आसान तरीका है। इसकी गणना करने के लिए, बस अपना उच्चतम स्कोर लें और उस उच्चतम स्कोर से अपना न्यूनतम स्कोर घटाएं। ऊपर के उदाहरण के लिए, 14 किग्रा - 11 किग्रा = 3 किग्रा। तो आप रिपोर्ट कर सकते हैं कि आप जिस वस्तु को माप रहे हैं वह है 12.4 किलो ± 3 किलो।
- ±3 किग्रा का मान आपका सटीक माप है। इसका मतलब है कि यह पैमाना केवल 6 किलो या 3 किलो भारी और 3 किलो हल्के की सीमा में ही सटीक है।
- ± प्रतीक को "अधिक या कम" के रूप में पढ़ा जा सकता है।
- सटीकता की गणना के लिए यह विधि सबसे अधिक इस्तेमाल की जाने वाली विधि है। हालांकि सरल, विडंबना यह है कि यह विधि बहुत सटीक नहीं है।
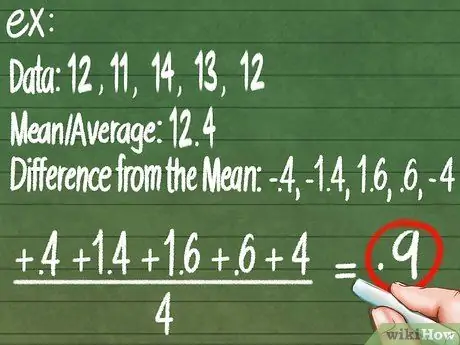
चरण 5. अधिक सटीक परिशुद्धता के लिए माध्य निरपेक्ष विचलन की गणना करें।
हमारे डेटा माध्य को फिर से देखें: 12.4 किग्रा। डेटा सेंटर से प्रत्येक माप कितनी दूर है, यह जानने के लिए प्रत्येक माप को माध्य से घटाएँ। सभी ऋणात्मक संख्याओं को धनात्मक बनाएं। उदाहरण के लिए:
आंकड़े:
12, 11, 14, 13, 12. मध्यमान औसत:
12, 4
माध्य से अंतर:
-0, 4; -1, 4; 1, 6; 0, 6; -0, 4"
. अब, इन संख्याओं का औसत ज्ञात कीजिए कि प्रत्येक माप का औसत केंद्र से कितनी दूर है:
(0, 4 + 1, 4 + 1, 6 + 0, 6 + 0, 4) / 5 = 0, 88. इसका मतलब यह है कि सामान्य तौर पर आप जो भी माप लेते हैं, वह आपके द्वारा देखे जाने वाले माप से ±0.88 किलोग्राम भिन्न हो सकता है।
आपको ऋणात्मक चिह्न को अनदेखा करना चाहिए अन्यथा मान एक दूसरे को रद्द कर देंगे। याद रखें कि ११, ४ और १३, ४ दोनों १२, ४ के औसत से १ किलो का अंतर हैं, केवल अंतर विपरीत (सकारात्मक या नकारात्मक) है।
टिप्स
- यदि आपका एक परीक्षण मान दूसरों की तुलना में अधिक या कम है, तो इस संख्या को अपनी गणना से बाहर न करें। भले ही यह मान एक त्रुटि है, यह डेटा है और इसका उपयोग सही गणना के लिए किया जाना चाहिए।
- अधिक सटीक गणना प्राप्त करने के लिए 5 से अधिक प्रयास करें। आप जितने अधिक प्रयोग करेंगे, आपको उतना ही सटीक मूल्य मिलेगा।







