भिन्नों की गिनती विकसित करने के लिए सबसे उपयोगी गणित कौशल में से एक है। भिन्नात्मक गणना करने से पहले, भिन्नों के भागों और प्रकारों की पहचान करना सीखें। उसके बाद, आप उन्हें जोड़ या घटा सकते हैं। अधिक जटिल गणनाओं के लिए, भिन्नों को गुणा और भाग करना सीखें। आमतौर पर, आपको भिन्नों को सरल या कम करने की भी आवश्यकता होगी।
कदम
विधि 1 में से 4: भिन्नों को पहचानना

चरण 1. भिन्न ज्ञात कीजिए।
भिन्नों को एक संख्या के रूप में विभाजित रेखा के ऊपर और दूसरी संख्या को रेखा के नीचे लिखा जाता है।
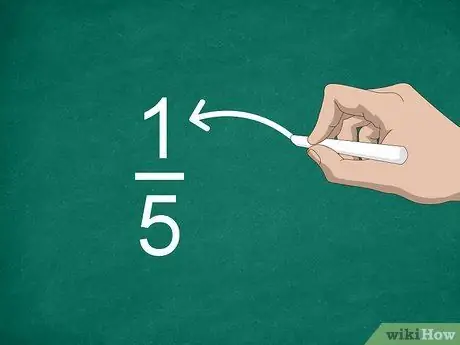
चरण 2. अंश को पहचानें।
रेखा के ऊपर की संख्या को अंश कहा जाता है और यह दर्शाता है कि भिन्न में कितने भाग हैं।
उदाहरण के लिए, भिन्न 1/5 में, "1" अंश है।
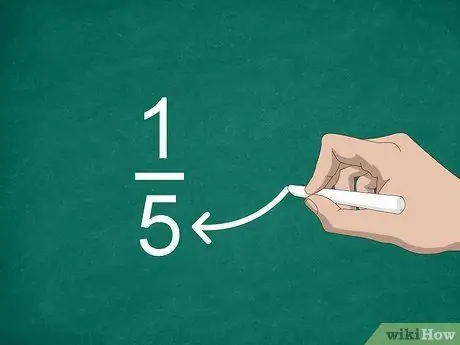
चरण 3. हर का पता लगाएं।
रेखा के नीचे रखी संख्या को हर कहते हैं। यह मान उन भागों की संख्या को इंगित करता है जो एक पूर्णांक "निर्माण" करते हैं।
उदाहरण के लिए, भिन्न 1/5 में, "5" हर है, इसलिए भिन्न के पाँच भाग हैं।

चरण 4. निर्धारित करें कि भिन्न उचित भिन्न हैं या अनुचित भिन्न।
यदि अंश हर से छोटा है, तो भिन्न एक प्राकृतिक भिन्न है। अनुचित भिन्नों में, अंश हर से बड़ा होता है।
- उदाहरण के लिए, 3/4 एक उचित भिन्न है और 5/3 एक अनुचित भिन्न है।
- यदि आपके पास एक पूर्णांक है जिसमें एक भिन्न शामिल है, तो संख्या को मिश्रित संख्या के रूप में जाना जाता है। उदाहरण के लिए, 1 1/2 एक मिश्रित संख्या है।
विधि 2 का 4: भिन्न जोड़ें या घटाएं

चरण 1. समान हर वाले भिन्नों को पहचानें।
यदि आपको भिन्नों को जोड़ने या घटाने की आवश्यकता है, तो गणना करने से पहले प्रत्येक अंश में समान भाजक होना चाहिए। यह सुनिश्चित करने के लिए कि वे सभी समान (समान) हैं, प्रत्येक भिन्न के हर का निरीक्षण करें।
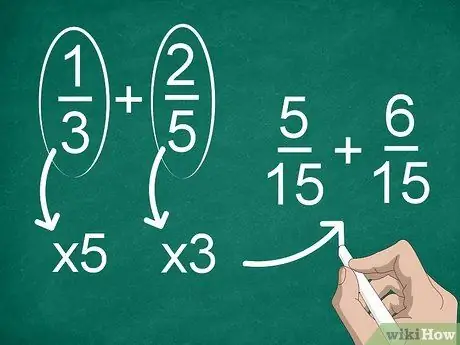
चरण 2. यदि प्रत्येक भिन्न का हर भिन्न है, तो एक उभयनिष्ठ हर ज्ञात कीजिए।
यदि हर समान नहीं हैं, तो आपको समान भाजक रखने के लिए भिन्नों को बदलना होगा। एक सामान्य हर को खोजने के लिए, प्रत्येक भिन्न को दूसरे के हर से गुणा करें।
उदाहरण के लिए, 1/3 + 2/5 में एक सामान्य भाजक खोजने के लिए, "1" और "3" को "5" से गुणा करें, फिर "2" और "5" को "3" से गुणा करें। अब, आपके पास 5/15 + 6/15 का योग है। उसके बाद, आप अंशों की गणना कर सकते हैं।
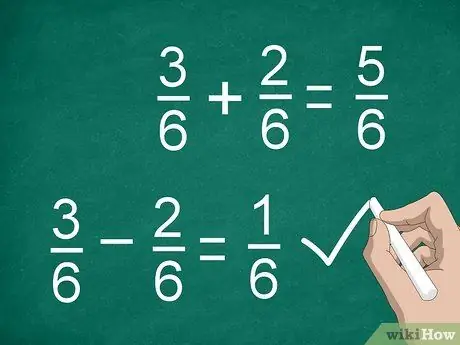
चरण 3. भिन्नों की गणना करने के लिए अंशों को जोड़ें या घटाएं।
एक बार जब आप एक सामान्य भाजक ढूंढ लेते हैं और अंशों को गुणा कर देते हैं (यदि आवश्यक हो), तो आप जोड़ने या घटाने के लिए तैयार हैं। अंशों को जोड़ें या घटाएं और परिणाम को विभाजन रेखा के ऊपर रखें। रेखा के नीचे सामान्य हर लिखिए।
- उदाहरण के लिए, 3/6 - 2/6 = 1/6।
- हरों को जोड़ें या घटाएं नहीं।
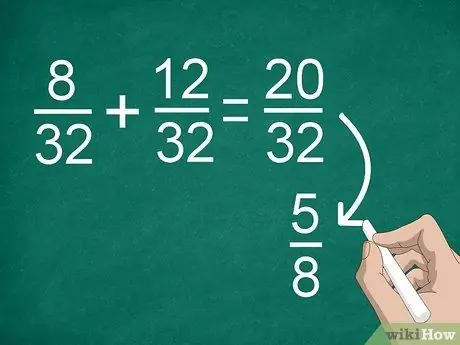
चरण 4. यदि आवश्यक हो तो परिणामों को सरल बनाएं।
यदि आपको पहले एक सामान्य भाजक खोजने की आवश्यकता थी, तो आपको एक बड़ा अंश मिल सकता है जिसे आप सरल बना सकते हैं। उदाहरण के लिए, यदि आप 8/32 +12/32 जोड़ते हैं, तो आपको परिणाम के रूप में "20/32" मिलेगा। इस अंश को "5/8" तक सरल बनाया जा सकता है।
विधि 3 का 4: भिन्नों का गुणा और सरलीकरण
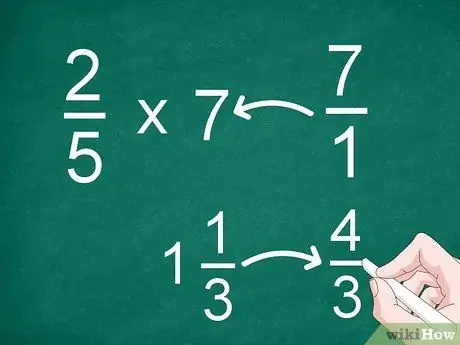
चरण 1. मिश्रित भिन्नों या पूर्णांकों को अनुचित भिन्नों में बदलें।
गुणन को आसान बनाने के लिए, आपको प्रत्येक संख्या को उचित या अनुचित भिन्न में बदलने की आवश्यकता है। यदि आपके पास पूर्ण संख्याएँ या मिश्रित संख्याएँ हैं जिन्हें गुणा करने की आवश्यकता है, तो पहले उन्हें एक सामान्य भिन्न (प्राकृतिक या अनुचित) में परिवर्तित करें।
- उदाहरण के लिए, 2/5 को 7 से गुणा करने के लिए, "7" को भिन्न में बदलें। उसके बाद, आप 2/5 को 7/1 से गुणा कर सकते हैं।
- यदि आपके पास 1 1/3 जैसी मिश्रित संख्या है, तो गुणा करने से पहले इसे एक अनुचित अंश ("4/3") में बदल दें।
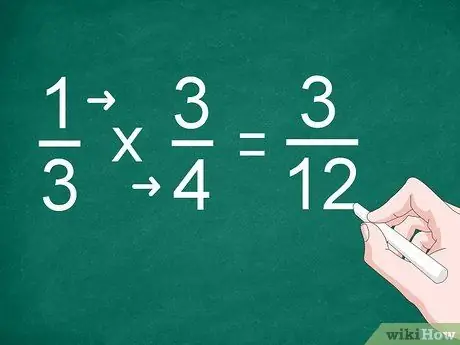
चरण 2. प्रत्येक अंश और हर को गुणा करें।
जोड़ करने के बजाय, अंश को गुणा करें और परिणाम को विभाजन रेखा के ऊपर लिखें। आपको हरों को गुणा करने और परिणाम को पंक्ति के नीचे लिखने की भी आवश्यकता है।
उदाहरण के लिए, 1/3 को 3/4 से गुणा करने के लिए, अंश प्राप्त करने के लिए "1" को "3" से गुणा करें। भाजक प्राप्त करने के लिए "3" को "4" से गुणा करें। गुणा का उत्तर "3/12" है।

चरण 3. परिणामों को सरल बनाएं।
आम तौर पर, आपको परिणाम को सरल रूप में कम करने की आवश्यकता होगी, खासकर यदि आपके पास शुरू में अप्राकृतिक अंश हैं। सबसे बड़ा सामान्य गुणनखंड ज्ञात कीजिए और अंश और हर को सरल बनाने के लिए उस गुणनखंड का उपयोग कीजिए।
उदाहरण के लिए, भिन्न 3/12 के लिए, "3" और "12" के बीच सबसे बड़ा सामान्य कारक "3" है। भिन्न के प्रत्येक अवयव को "3" से तब तक विभाजित करें जब तक आपको भिन्न "1/4" प्राप्त न हो जाए।
विधि 4 का 4: भिन्नों को विभाजित करें
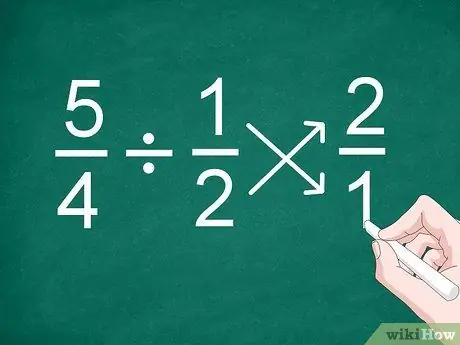
चरण 1. दूसरे भिन्न की स्थिति को उलट दें।
भिन्नों को विभाजित करने का सबसे आसान तरीका, यहां तक कि भिन्न हर वाले भिन्न, परिणाम की गणना करने से पहले दूसरे अंश की स्थिति को उलट देना है।
उदाहरण के लिए, समस्या 5/4 1/2 के लिए, भिन्न "1/2" की स्थिति को "2/1" बनने के लिए उलट दें।
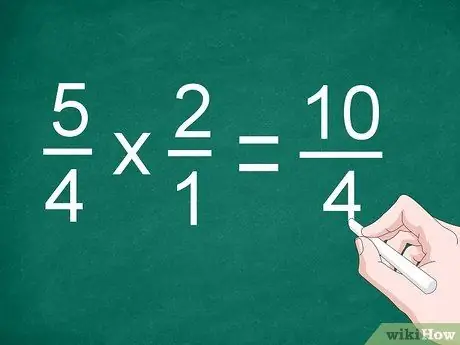
चरण 2. अंश और हर को गुणा करें।
अंशों को गुणा करने के लिए अंशों को सीधे गुणा करें। परिणाम को विभाजन रेखा के ऊपर लिखें, फिर हर को गुणा करें। रेखा के नीचे हर के गुणनफल को रिकॉर्ड करें।
पिछले उदाहरण के लिए, "10/4" प्राप्त करने के लिए 5/4 को 2/1 से गुणा करें।
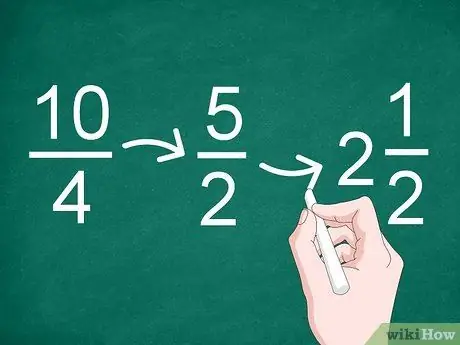
चरण 3. यदि आवश्यक हो तो परिणामों को सरल बनाएं।
यदि विभाजन का परिणाम एक अनुचित भिन्न है या घटाया जा सकता है, तो भिन्न को सरल करें। भिन्न को कम करने के लिए सबसे बड़े सामान्य कारक का उपयोग करें।
- उदाहरण के लिए, भिन्न 10/4 में सबसे बड़ा सामान्य कारक "2" है, इसलिए सरलीकरण का परिणाम "5/2" हो जाता है (10 को 2 से विभाजित किया जाता है, और 4 को 2 से विभाजित किया जाता है)।
- चूंकि सरलीकरण का परिणाम एक अनुचित अंश है, आप इसे एक पूर्णांक और एक भिन्न (एक मिश्रित संख्या) में बदल सकते हैं। इसलिए, 5/2 को "2" में बदला जा सकता है।
टिप्स
- यदि आप जटिल भिन्नों के साथ काम कर रहे हैं, तो आपको भिन्न को सरल बनाने के लिए कुछ अतिरिक्त कदम उठाने होंगे। हालाँकि, यह सरलीकरण ही गणना प्रक्रिया का एक अनिवार्य हिस्सा है।
- गलत गणना के जोखिम को कम करने के लिए हमेशा भिन्नों को साफ-सुथरा लिखें।







