अधिकांश लोगों के लिए, भिन्न पहली जटिल गणनाएँ होती हैं जिनका सामना करना पड़ता है। भिन्नों की अवधारणा काफी कठिन है और इसे करने के लिए आपको विशेष परिस्थितियों को सीखने की आवश्यकता होती है। क्योंकि भिन्नों में जोड़, घटाव, गुणा और भाग के लिए विशेष नियम होते हैं, बहुत से लोग इसके बारे में भ्रमित होते हैं। हालांकि, बहुत सारे अभ्यास के साथ, कोई भी भिन्नों से संबंधित गणनाओं को सीख सकता है और पूरा कर सकता है।
कदम
5 में से विधि 1: भिन्नों को समझना
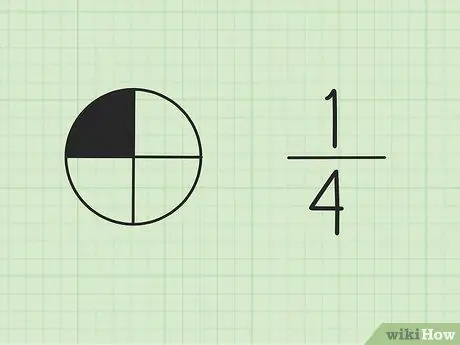
चरण 1. समझें कि भिन्न पूरे का हिस्सा हैं।
शीर्ष पर संख्या को अंश कहा जाता है, और कुल के भागों की संख्या का प्रतिनिधित्व करता है। नीचे की संख्या को हर कहा जाता है, जो भागों की कुल संख्या का प्रतिनिधित्व करता है।
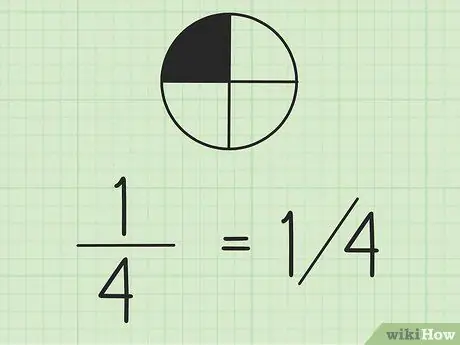
चरण 2. ध्यान रखें कि आप स्लैश का उपयोग करके भिन्न लिख सकते हैं।
बाईं ओर की संख्या अंश है और दाईं ओर की संख्या हर है। यदि आप एक ही पंक्ति में भिन्नों के साथ काम कर रहे हैं, तो हर के ऊपर अंश लिखना एक अच्छा विचार है।
उदाहरण के लिए, यदि आप चार पिज्जा स्लाइस में से एक लेते हैं, तो आपके पास पिज्जा है। अगर आपके पास 7/3 पिज़्ज़ा है, तो इसका मतलब है कि आपके पास दो पूरे पिज़्ज़ा और 3 में से 1 पिज़्ज़ा है।
5 की विधि 2: मिश्रित और साधारण भिन्नों के बीच अंतर

चरण 1. समझें कि मिश्रित संख्याओं में पूर्ण संख्याएं और भिन्न होते हैं, उदाहरण के लिए 2 1/3 या 45 1/2।
आमतौर पर, आपको मिश्रित संख्याओं को जोड़ने, घटाने, गुणा करने या विभाजित करने के लिए एक सरल रूप में परिवर्तित करना होता है।

चरण 2. भिन्न में हर से पूर्ण संख्या को गुणा करके, फिर अंश से जोड़कर मिश्रित संख्या को बदलें।
परिणाम को अंश के रूप में लिखें, जबकि हर नहीं बदलता है।
उदाहरण के लिए, 2 1/3 को साधारण भिन्न में बदलने के लिए, 2 को 3 से गुणा करें, फिर 1 जोड़ें और 7/3 प्राप्त करें।

चरण 3. अंश को हर से भाग देकर साधारण भिन्नों को मिश्रित संख्याओं में बदलें।
भाग के पूरे परिणाम को एक पूर्णांक के रूप में लिखा जाता है, और शेष भाग को भिन्न के अंश के रूप में लिखा जाता है। भाजक नहीं बदलता है।
उदाहरण के लिए, 7/3 को एक मिश्रित संख्या में बदलने के लिए, 7 को 3 से भाग देकर 2 प्राप्त करने के लिए शेष 1 प्राप्त करें। तो मिश्रित संख्या 2 1/3 है। साधारण भिन्नों को केवल मिश्रित संख्याओं में परिवर्तित किया जा सकता है यदि अंश हर से बड़ा हो।
विधि 3 का 5: भिन्नों को जोड़ना और घटाना
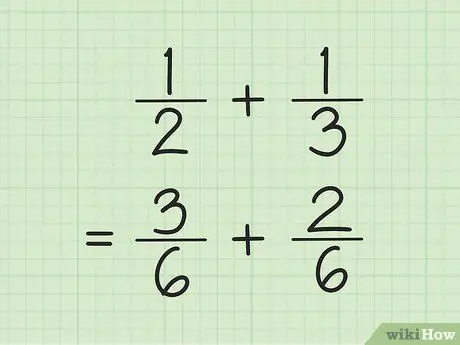
चरण 1. भिन्नों को जोड़ने और घटाने के लिए एक सामान्य हर खोजें।
चाल, हर में संख्याओं को गुणा करें, फिर हर अंश को हर को खोजने के लिए उपयोग की गई संख्या से गुणा करें। कभी-कभी, आप हर को एक दूसरे से गुणा करके हर के लिए एलसीएम (कम से कम सामान्य गुणक) पा सकते हैं।
उदाहरण के लिए, जोड़ने और 1/3 के लिए, पहले दो हरों के एलसीएम (कम से कम सामान्य गुणक) को एक दूसरे को गुणा करके खोजें। इस प्रकार, आप LCM 6 प्राप्त करने के लिए 2 और 3 को गुणा करते हैं। पहली भिन्न के नए अंश के रूप में 3 प्राप्त करने के लिए 1 को 3 से गुणा करें। दूसरी भिन्न के नए अंश के रूप में 2 प्राप्त करने के लिए 1 को 2 से गुणा करें। आपके नए भिन्न 3/6 और 2/6 हैं।
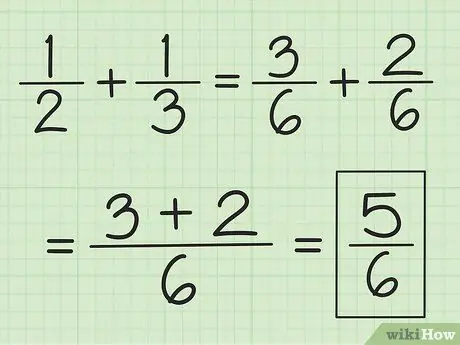
चरण 2. दो अंशों को एक साथ जोड़ें और हर को न बदलें।
उदाहरण के लिए, 3/6 जमा 2/6 5/6 है, और 2/6 जमा 1/6 3/6 है।
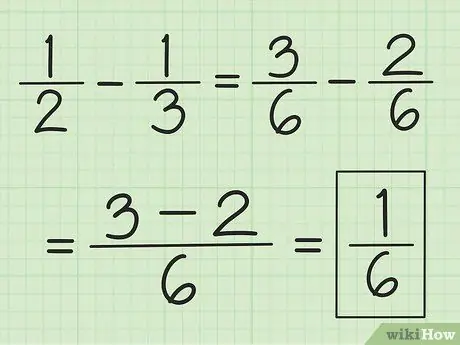
चरण 3. घटाव के लिए इसी तरह की तकनीक का उपयोग करें।
पहले हर के एलसीएम का पता लगाएं, लेकिन उन्हें जोड़ने के बजाय, पहले अंश की संख्या को दूसरे की संख्या से घटाएं।
उदाहरण के लिए, 1/2 से 1/3 घटाने के लिए, पहले भिन्नों को 3/6 और 2/6 में बदलें, फिर 3 को 2 से घटाकर 1 प्राप्त करें। इसका परिणाम 1/6 होता है।
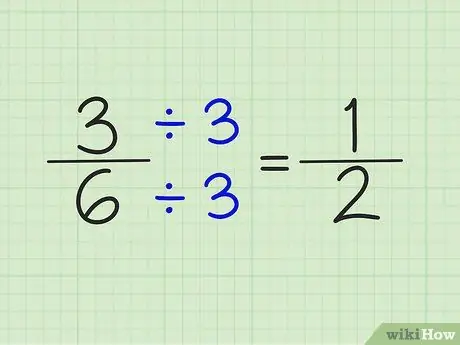
चरण 4. अंश और हर को समान संख्या से विभाजित करके भिन्नों को सरल कीजिए।
उदाहरण के लिए, संख्या 5/6 को सरल नहीं बनाया जा सकता है। हालांकि, अंश और हर को संख्या 3 से विभाजित करके 3/6 को सरल बनाया जा सकता है। परिणाम 1/2 का एक अंश है।

चरण 5. भिन्न को मिश्रित संख्या में परिवर्तित करें यदि अंश हर से बड़ा है।
5 की विधि 4: भिन्नों का गुणा और भाग करें
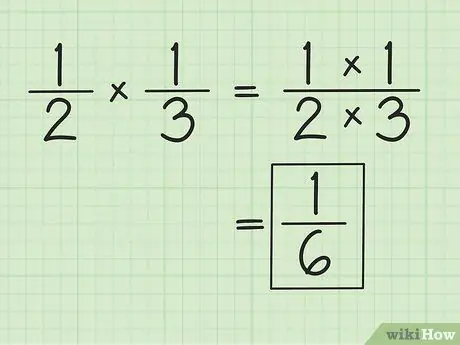
चरण 1. भिन्नों को गुणा करने के लिए अंश और हर को अलग-अलग गुणा करें।
उदाहरण के लिए, जब गुणा और 1/3 किया जाता है, तो परिणाम 1/6 (1 गुना 1, और 2 गुना 3) होता है। भिन्नों को गुणा करते समय आपको हरों का मिलान करने की आवश्यकता नहीं है। यदि आवश्यक हो तो प्राप्त परिणामों को सरल या संशोधित करें।
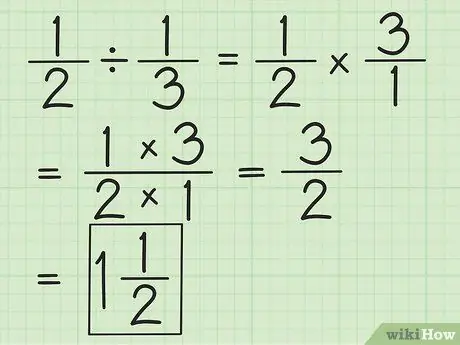
चरण 2. दो भिन्नों को दूसरी भिन्न को उल्टा करके, फिर दोनों को गुणा करके विभाजित करें।
उदाहरण के लिए, यदि आप 1/2 को 1/3 से भाग देना चाहते हैं, तो पहले दूसरे भिन्न को 3/1 पर उल्टा कर दें। 3/1 से गुणा करें और 3/2 प्राप्त करें। भिन्नों को सरल करें या यदि संभव हो तो मिश्रित संख्याओं में परिवर्तित करें।
विधि 5 में से 5: जटिल भिन्नों के साथ कार्य करना
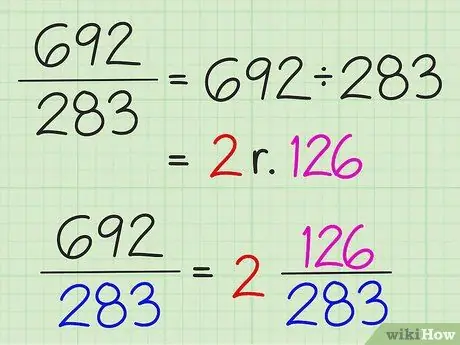
चरण 1. सभी भिन्नों को समान रूप से कार्य करें, भले ही समस्या बहुत जटिल लगे।
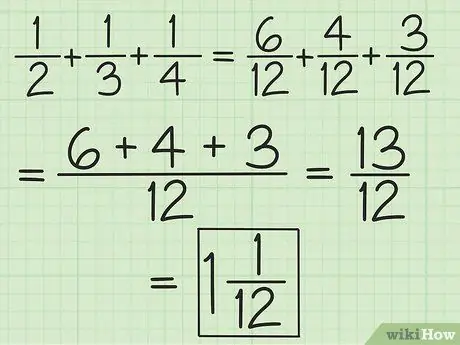
चरण 2. सभी भिन्नों के हरों का मिलान करें या दो से अधिक भिन्नों को जोड़ने और घटाने के लिए बाएं से दाएं जोड़े में काम करें।
उदाहरण के लिए, १/२, १/३ और १/४ को जोड़ने के लिए, आप १३/१२ प्राप्त करने के लिए उन्हें ६/१२, ४/१२, और ३/१२ में बदल सकते हैं, या आप ३/६ और २ जोड़ सकते हैं / 6 तो आपको 5/6 मिलता है, फिर 5/6 और 1/4 जोड़ें (हरों को बराबर करें ताकि दूसरा अंश 3/12 हो जाए) 13/12 (10/12 प्लस 3/12) प्राप्त करने के लिए। इसे एक मिश्रित संख्या में बदलें, जो 1 1/12 है।
टिप्स
- याद रखें कि आपने काफी गणित सीखा है। गणित एक ऐसी भाषा की तरह है जिसका आप धाराप्रवाह उच्चारण कर सकते हैं, और अब आप इसे पढ़ना और लिखना सीखने की कोशिश कर रहे हैं।
- अपनी गणना के अंतिम परिणाम को हमेशा सरल बनाना याद रखें, चाहे आपकी समस्या एक साधारण भिन्न के रूप में हो, एक मिश्रित संख्या के रूप में हो, या एक जटिल भिन्न के रूप में हो।







