कैलकुलेटर के बिना वर्गमूल खोजने के 3 तरीके

2024 लेखक: Jason Gerald | [email protected]. अंतिम बार संशोधित: 2023-12-16 11:13

किसी संख्या का वर्गमूल ज्ञात करना आसान है यदि उत्तर एक पूर्णांक है। यदि उत्तर एक पूर्णांक नहीं है, तो वर्गमूल प्राप्त करने के लिए आप कई प्रक्रियाओं का पालन कर सकते हैं, भले ही आप कैलकुलेटर का उपयोग न करें। इसके लिए आपको गुणा, जोड़ और भाग की मूल बातें समझनी होंगी।

कदम

विधि 1 का 3: एक पूर्णांक का वर्गमूल ज्ञात करना

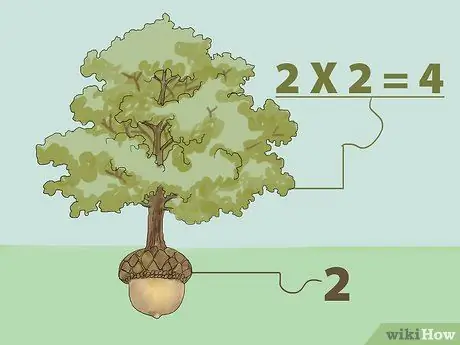
चरण 1. गुणा करके पूर्ण वर्गमूल ज्ञात कीजिए।

किसी संख्या का वर्गमूल वह संख्या होती है जिसे अपने आप से गुणा करने पर मूल संख्या वापस आ जाती है। दूसरे शब्दों में: "हम जो संख्या चाहते हैं उसे प्राप्त करने के लिए हम किस संख्या से गुणा कर सकते हैं?"

• उदाहरण के लिए, 1 का वर्गमूल 1 है क्योंकि 1 को 1 से गुणा करने पर 1 (1X1=1) होता है। इस प्रकार, 4 का वर्गमूल 2 है क्योंकि 2 को 2 से गुणा करने पर 4 (2X2=4) होता है। एक पेड़ के रूप में वर्गमूल अवधारणा के बारे में सोचें। बीज से एक पेड़ उगता है। तो, एक पेड़ एक बीज से बड़ा होता है, जो एक बीज से उगता है जो कि इसकी जड़ है। ऊपर के उदाहरण से, 4 पेड़ है, और 2 बीज है।
• तो, 9 का वर्गमूल 3 (3X3=9) है, 16 का 4 (4X4=16) है, 25 का 5 (5X5=25) है, 36 का 6 (6X6=36) है, 49 का 7 है (7X7 =49), 64 से 8 (8X8=64), 81 से 9 (9X9=81) है, और 100 से 10 (10X10=100) है।

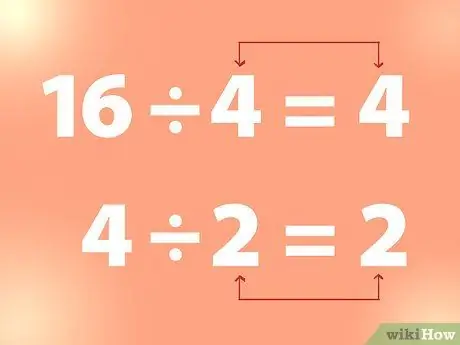
चरण 2. वर्गमूल ज्ञात करने के लिए सतत विभाजन का प्रयोग करें।

किसी पूर्णांक का वर्गमूल ज्ञात करने के लिए, आप पूर्णांक को किसी संख्या से तब तक विभाजित कर सकते हैं जब तक कि आपको भाजक के बराबर कोई संख्या न मिल जाए।

• उदाहरण: 16 को 4 से भाग देने पर 4 होता है और 4 को 2 से भाग देने पर 2 होता है, और इसी तरह आगे भी। इस प्रकार, उपरोक्त उदाहरण से, 4, 16 का वर्गमूल है और 2, 4 का वर्गमूल है।
• पूर्ण वर्गमूल में कोई भिन्न या दशमलव नहीं होता क्योंकि वे पूर्ण संख्याएँ होती हैं।

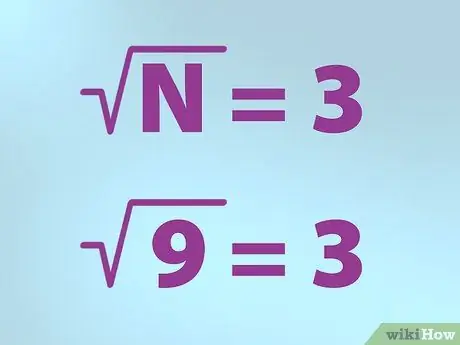
चरण 3. वर्गमूल के लिए सही चिन्ह का प्रयोग करें।

गणितज्ञ वर्गमूल का प्रतिनिधित्व करने के लिए एक विशेष प्रतीक का उपयोग करते हैं। आकार एक चेक मार्क की तरह है जिसमें शीर्ष दाईं ओर एक रेखा है।

• N उस संख्या के बराबर है जिसके लिए आप वर्गमूल निकालना चाहते हैं। N को चेक मार्क के नीचे रखा गया है।
• इसलिए, यदि आप 9 का वर्गमूल निकालना चाहते हैं, तो एक चेक मार्क (प्रतीक "रूट") के अंदर "N" (9) डालकर एक सूत्र लिखें, फिर एक समान चिह्न लिखें और उसके बाद 3 लिखें। इसका अर्थ है "वर्गमूल" 9 3" के बराबर है।

विधि 2 का 3: किसी अन्य संख्या का वर्गमूल ज्ञात करना

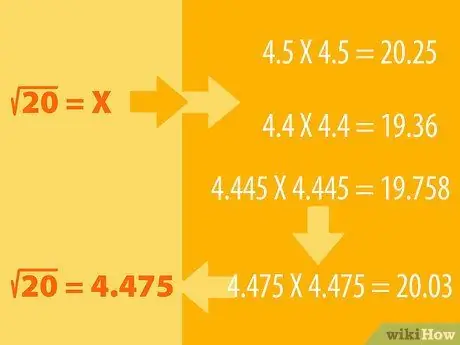
चरण 1. अनुमान लगाएं, और उन्मूलन की प्रक्रिया करें।

एक गैर-पूर्णांक संख्या का वर्गमूल ज्ञात करना कठिन है। हालांकि, इसका मतलब यह नहीं है कि यह असंभव है।

• उदाहरण के लिए, मान लें कि आप 20 का वर्गमूल निकालना चाहते हैं। हम जानते हैं कि 16 एक पूर्ण वर्ग है जिसका वर्गमूल 4 (4X4=16) है। फिर 25 वर्गमूल 5 (5X5=25) हैं, इसलिए 20 का वर्गमूल दोनों के बीच होना चाहिए।
• आप अनुमान लगा सकते हैं कि 20 का वर्गमूल 4.5 है। अब परिणाम देखने के लिए 4.5 का वर्ग करें। यानी, हम 4, 5 को अपने आप से गुणा करते हैं: 4, 5X4, 5। देखें कि उत्तर 20 से अधिक है या कम। यदि आपका अनुमान बहुत दूर है, तो दूसरी संख्या आज़माएं (जैसे 4, 6 या 4, 4) और समायोजित करें उसी के अनुसार अनुमान लगाएं। जब तक आपको नंबर 20 नहीं मिल जाता।
• उदाहरण के लिए, 4, 5X4, 5 = 20, 25, इसलिए तार्किक रूप से हमें एक छोटी संख्या ज्ञात करनी होगी, शायद 4, 4. 4, 4X4, 4 = 19, 36. तो, 20 का वर्गमूल 4 के बीच होना चाहिए, 5 और 4, 4. 4, 445X4, 445 के साथ प्रयास करें। परिणाम 19, 758 है। परिणाम करीब आ रहा है। 4, 475X4, 475 = 20, 03 प्राप्त होने तक अन्य संख्याओं के साथ प्रयास करते रहें। पूर्णांकित करने पर, वह संख्या 20 के बराबर होती है।

चरण 2. औसत प्रक्रिया का प्रयोग करें।

यह प्रक्रिया उन दो निकटतम पूर्ण वर्गों को खोजने से भी शुरू होती है जो संख्या से घिरे हुए हैं।

• फिर उस संख्या को किसी एक पूर्ण वर्गमूल से भाग दें। उत्तर लें, फिर उस संख्या और उस संख्या के बीच का औसत ज्ञात करें जिसका मूल आप खोजना चाहते हैं (आप दोनों को एक साथ जोड़कर और दो से विभाजित करके औसत ज्ञात कर सकते हैं)। फिर प्रारंभिक संख्या को प्राप्त औसत से विभाजित करें। अंतिम चरण, पहली बार गणना किए गए औसत के साथ परिणामों का औसत ज्ञात करें।
• ध्वनि जटिल? एक उदाहरण दिया जाए तो यह आसान होगा। उदाहरण के लिए, 10 दो पूर्ण वर्गों 9 (3X3=9) और 16 (4X4=16) के बीच स्थित है। दोनों संख्याओं का वर्गमूल 3 और 4 है। अतः, 10 को पहली संख्या से भाग दें, 3. परिणाम 3, 33 है। अब 3 और 3, 33 को एक साथ जोड़कर और 2 से विभाजित करके औसत ज्ञात करें। परिणाम 3 है, 1667 अब 10 को 3.1667 से विभाजित करें। परिणाम 3.1579 है। फिर 3.1579 और 3.1667 का औसत उन्हें जोड़कर और 2 से विभाजित करके ज्ञात करें। परिणाम 3.1623 है।
• उत्तर को (इस उदाहरण 3, 1623 में) स्वयं से गुणा करके अपना परिणाम देखें। 3.1623 को 3.1623 से गुणा करने पर 10.001 का परिणाम प्राप्त होता है।

विधि 3 का 3: ऋणात्मक संख्याओं का वर्ग करना

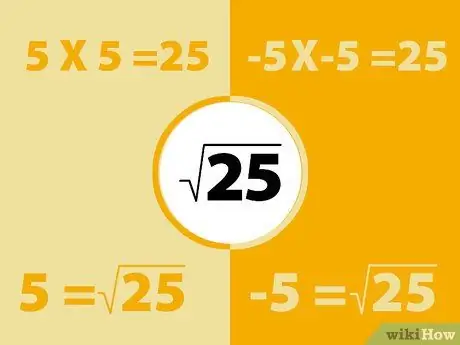
चरण 1. उसी विधि का उपयोग करके ऋणात्मक संख्याओं का वर्ग करें।

याद रखें कि नकारात्मक समय सकारात्मक होता है। तो, एक ऋणात्मक संख्या का वर्ग एक धनात्मक संख्या उत्पन्न करेगा।

• उदाहरण के लिए, -5X-5 = 25. हालांकि, यह भी याद रखें कि 5x5=25. तो 25 का वर्गमूल -5 या 5 हो सकता है। मूल रूप से प्रत्येक संख्या के दो वर्गमूल होते हैं।
• इसी तरह, 3X3=9 और -3X-3=9, इसलिए 9 के वर्गमूल 3 और -3 हैं। धनात्मक वर्गमूल को "प्रमुख मूल" कहा जाता है। इस बिंदु पर, हमें केवल इस उत्तर पर ध्यान देने की आवश्यकता है।

चरण 2. एक कैलकुलेटर का प्रयोग करें।

जबकि हाथ से गणित करना सबसे अच्छा है, वर्गमूल की गणना के लिए कई ऑनलाइन कैलकुलेटर उपलब्ध हैं।

• एक नियमित कैलकुलेटर पर वर्गमूल बटन देखें।
• ऑनलाइन कैलकुलेटर में, सीधे वह संख्या दर्ज करें जिसके लिए आप वर्गमूल मान ज्ञात करना चाहते हैं और बटन पर क्लिक करें। कंप्यूटर आपको वर्गमूल मान दिखाएगा।

टिप्स

• कुछ महत्वपूर्ण पूर्ण वर्गों को हमेशा ध्यान में रखें:

  • 0² = 0, 1² = 1, 3² = 9, 4² = 16, 5² = 25, 6² = 36, 7² = 49, 8² = 64, 9² = 81, 10² = 100,
  • यह पूर्ण वर्ग भी याद रखें: 11² = 121, 12² = 144, 13² 169, 14² = 196, 15² = 225, 16² = 256, 17² = 289…
  • यह भी नोट करें: 10² = 100, 20² = 400, 30² = 900, 40² = 1600, 50² = 2500, …