भौतिकी में विस्थापन किसी वस्तु की स्थिति में परिवर्तन को दर्शाता है। जब आप विस्थापन की गणना करते हैं, तो आप गणना करते हैं कि कोई वस्तु अपने प्रारंभिक और अंतिम स्थानों के आधार पर कितनी दूर है। विस्थापन की गणना के लिए आप जिस सूत्र का उपयोग करते हैं वह समस्या को दिए गए चर पर निर्भर करता है। विस्थापन की गणना के लिए इन चरणों का पालन करें।
कदम
5 का भाग 1: परिणामी विस्थापन की गणना

चरण 1. परिणामी विस्थापन सूत्र का उपयोग करें यदि दूरी की इकाई का उपयोग आपके आरंभ और समाप्ति स्थानों को इंगित करने के लिए किया जाता है।
हालांकि दूरी विस्थापन से अलग है, परिणामी विस्थापन समस्या यह देखती है कि वस्तु ने कितने किलोमीटर या मीटर की यात्रा की है। आप विस्थापन की गणना करने के लिए माप की इस इकाई का उपयोग करेंगे और किसी वस्तु का स्थान उसके प्रारंभिक बिंदु से कितनी दूर भटक जाएगा।
- परिणामी विस्थापन सूत्र इस प्रकार लिखा जाता है: एस = एक्स²+वाई². एस विस्थापन है। X वस्तु की गति की पहली दिशा है और Y वस्तु की गति की दूसरी दिशा है। यदि आपकी वस्तु केवल एक दिशा में चलती है, तो Y = 0.
- एक वस्तु अधिकतम दो दिशाओं में ही चल सकती है क्योंकि उत्तर/दक्षिण या पूर्व/पश्चिम अक्ष के साथ गति करना तटस्थ गति मानी जाती है।

चरण 2. गति के क्रम में डॉट्स कनेक्ट करें और उन्हें ए-जेड से लेबल करें।
एक बिंदु से दूसरे बिंदु तक एक सीधी रेखा खींचने के लिए एक रूलर का उपयोग करें।
- एक सीधी रेखा का उपयोग करके अपने शुरुआती बिंदु को अपने अंतिम बिंदु से जोड़ना भी याद रखें। यह वह विस्थापन है जिसकी हम गणना करेंगे।
- उदाहरण के लिए, यदि कोई वस्तु 300 मीटर पूर्व और उत्तर 400 मीटर चलती है, तो वह एक समकोण त्रिभुज बनाएगी। AB त्रिभुज का पहला चरण होगा और BC दूसरा चरण होगा। AC त्रिभुज का कर्ण होगा और इसका परिमाण वस्तु का विस्थापन है। इस उदाहरण में, दो दिशाएँ पूर्व और उत्तर हैं।

चरण 3. x² और y² के लिए मान दर्ज करें।
अब जब आप अपनी वस्तु की गति की दो दिशाओं को जानते हैं, तो मानों को उपयुक्त चरों में दर्ज करें।
उदाहरण के लिए, x = ३०० और y = ४००। आपका सूत्र इस तरह दिखना चाहिए: S = ३००² + ४००²।
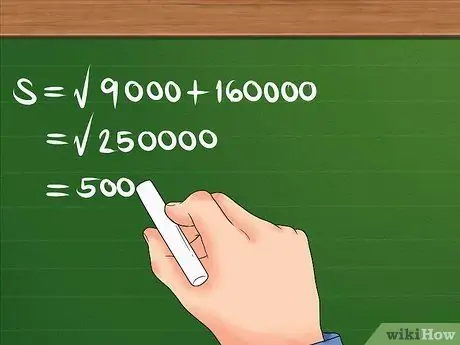
चरण 4. संचालन के क्रम का उपयोग करके सूत्र की गणना करें।
पहले 300 और 400 का वर्ग करें, फिर उन्हें जोड़ दें, और योग का वर्गमूल ज्ञात करें।
उदाहरण के लिए: एस = ९०००० + १६००००। एस = २५००००। एस = 500। अब आप जानते हैं कि विस्थापन 500 मीटर है।
5 का भाग 2 जब गति और समय ज्ञात हो

चरण 1. इस सूत्र का उपयोग तब करें जब समस्या आपको किसी वस्तु की गति और उसमें लगने वाले समय के बारे में बताए।
कुछ गणित के प्रश्न आपको यह नहीं बताएंगे कि कोई वस्तु कितनी दूर या कितनी तेजी से आगे बढ़ रही है। आप समय और गति के इस परिमाण का उपयोग करके विस्थापन की गणना कर सकते हैं।
-
इस मामले में, सूत्र बन जाता है: एस = 1/2 (यू + वी) टी।
यू = वस्तु का प्रारंभिक वेग, या वस्तु कितनी तेजी से एक निश्चित दिशा में चलना शुरू करती है। वी = वस्तु का अंतिम वेग, या वस्तु कितनी तेजी से अपने अंतिम स्थान की ओर बढ़ रही है। T = वस्तु को अपने अंतिम स्थान तक पहुँचने में लगने वाला समय।
- उदाहरण: एक कार सड़क पर 45 सेकंड (आवश्यक समय) के लिए नीचे जाती है। कार 20 मीटर/सेकंड (प्रारंभिक गति) से पश्चिम की ओर मुड़ रही है और सड़क के अंत में, इसकी गति 23 मीटर/सेकंड (अंतिम गति) है। इन कारकों के आधार पर विस्थापन की गणना कीजिए।

चरण 2. उपयुक्त चरों में आवश्यक गति और समय दर्ज करें।
अब जब आप जानते हैं कि कार कितनी दूर चल रही है, कार कितनी तेजी से शुरू और अंत में चल रही है, तो आप शुरुआती स्थान से अंतिम स्थान तक की दूरी का पता लगा सकते हैं।
आपका फॉर्मूला इस तरह दिखना चाहिए: S = 1/2(20 + 23)45।

चरण 3. मानों को सही स्थान पर रखने के बाद सूत्र की गणना करें।
संचालन के क्रम का पालन करना याद रखें, अन्यथा विस्थापन के परिणामस्वरूप बहुत भिन्न मान होंगे।
- इस फॉर्मूले के लिए, इससे कोई फर्क नहीं पड़ता कि आप गलती से स्टार्टिंग और एंडिंग स्पीड को स्वैप कर देते हैं। चूंकि आप पहले इन नंबरों को एक साथ जोड़ रहे हैं, इससे कोई फर्क नहीं पड़ता कि वे कोष्ठक में कहां हैं। हालांकि, अन्य सूत्रों के लिए, प्रारंभिक और अंतिम वेगों की अदला-बदली के परिणामस्वरूप अलग-अलग विस्थापन मान होंगे।
- आपका सूत्र इस तरह दिखना चाहिए: S = 1/2(43)45। पहले 43 को 2 से विभाजित करें, जिसके परिणामस्वरूप 21, 5 प्राप्त होता है। फिर 21, 5 को 45 से गुणा करें, तो परिणाम 967.5 मीटर है। 967, 5 आपके विस्थापन का परिमाण है, या आपकी कार अपने शुरुआती बिंदु से कितनी दूर चली गई है।
भाग ३ का ५: जब प्रारंभिक वेग, त्वरण और समय ज्ञात हो
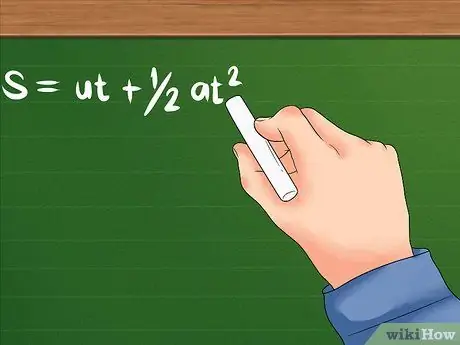
चरण 1. संशोधित सूत्र का प्रयोग करें जब प्रारंभिक वेग और समय के अतिरिक्त त्वरण ज्ञात हो।
कुछ प्रश्न आपको केवल यह बताएंगे कि शुरुआत में वस्तु कितनी तेजी से आगे बढ़ रही है, वस्तु कितनी तेजी से गति करना शुरू कर रही है और वस्तु कितनी दूर जा रही है। आपको निम्न सूत्र की आवश्यकता होगी।
- इस समस्या का सूत्र है: एस = यूटी + 1/2at². यू अभी भी प्रारंभिक गति को इंगित करता है; a वस्तु का त्वरण है, या उसका वेग कितनी तेजी से बदलना शुरू होता है। T का अर्थ उस समय से हो सकता है जो किसी वस्तु को गति देने में लगता है या एक निश्चित समय लेता है। दोनों समय इकाइयों जैसे सेकंड, घंटे और अन्य का उपयोग करेंगे।
- मान लीजिए कि 25 m/s (प्रारंभिक वेग) से गतिमान एक कार 4 सेकंड (समय) के लिए 3 m/s2 (त्वरण) से गति करना शुरू करती है। 4 सेकंड के बाद कार का विस्थापन क्या है?

चरण 2. सूत्र में मान दर्ज करें।
पिछले फॉर्मूले के विपरीत, यहां केवल प्रारंभिक गति का प्रतिनिधित्व किया जाता है, इसलिए सही डेटा दर्ज करना सुनिश्चित करें।
उपरोक्त नमूना डेटा के आधार पर, आपका सूत्र इस तरह दिखेगा: S = 25(4) + 1/2(3)4²। यह संख्याओं को अलग करने में आपकी मदद करने के लिए आपके त्वरण परिमाण और समय के चारों ओर कोष्ठक जोड़ने में मदद करता है।
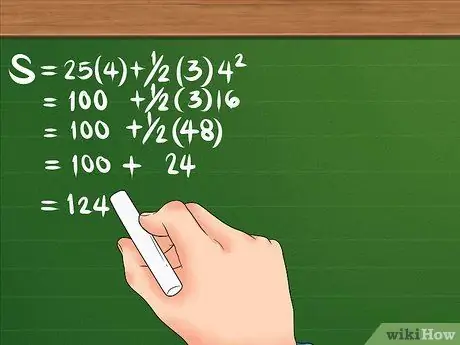
चरण 3. संचालन के सही क्रम में करते हुए विस्थापन की गणना करें।
संचालन के क्रम को याद रखने में आपकी मदद करने का एक त्वरित तरीका है गधा पुल कुर इर कुआ सी कदंग बा वा जुरागन कछुए। यह सही क्रम का प्रतिनिधित्व करता है: कोष्ठक, वर्ग, गुणा, भाग, जोड़ और घटाव।
आइए फिर से सूत्र को देखें: S = 25(4) + 1/2(3)4²। पहले, वर्ग ४, परिणाम १६ है। फिर, १६ को ३ से गुणा करें, जिससे ४८ बनते हैं; फिर 25 को 4 से गुणा करके 100 बना लें। 48 को 2 से विभाजित करके 24 बना लें। आपका समीकरण इस तरह दिखना चाहिए: S = 100 + 24। एक बार जब आप दोनों को एक साथ जोड़ देते हैं, तो विस्थापन 124 मीटर हो जाता है।
भाग ४ का ५: कोणीय विस्थापन की गणना करना

चरण 1. कोणीय विस्थापन का पता लगाएं क्योंकि वस्तु एक वृत्ताकार पथ में चलती है।
यद्यपि आप अभी भी एक सीधी रेखा का उपयोग करके विस्थापन की गणना कर रहे होंगे, आपको वस्तु के आरंभ और अंत स्थानों के बीच अंतर खोजने की आवश्यकता होगी क्योंकि यह एक गोलाकार पथ में चलती है।
- कल्पना कीजिए कि एक लड़की मीरा-गो-राउंड पर बैठी है। जैसे ही वह हिंडोला के साथ घूमता है, वह एक वृत्ताकार पथ में चलेगा। कोणीय विस्थापन प्रारंभिक और अंतिम स्थानों के बीच सबसे छोटी दूरी खोजने का प्रयास करता है जब वस्तु एक सीधी रेखा में नहीं चल रही हो।
- कोणीय विस्थापन का सूत्र है: = एस/आर जहाँ S रैखिक विस्थापन है, r त्रिज्या है, और कोणीय विस्थापन है। रैखिक विस्थापन एक चाप के साथ एक वस्तु कितनी दूर चलती है। त्रिज्या वृत्त के केंद्र से वस्तु की दूरी है। कोणीय विस्थापन वह मान है जिसे हम खोजना चाहते हैं।

चरण 2. रैखिक विस्थापन और त्रिज्या को समीकरण में प्लग करें।
याद रखें कि त्रिज्या वृत्त के केंद्र से दूरी है; कुछ समस्याएँ आपको एक वृत्त का व्यास बताएगी, जिसे त्रिज्या ज्ञात करने के लिए 2 से विभाजित करना होगा।
- यहाँ एक समस्या का उदाहरण दिया गया है: एक लड़की मीरा-गो-राउंड की सवारी करती है। सीट सर्कल के केंद्र (त्रिज्या) से 1 मीटर की दूरी पर है। यदि लड़की 1.5 मीटर (रैखिक विस्थापन) के एक चाप प्रक्षेपवक्र में चल रही है, तो उसका कोणीय विस्थापन क्या है?
- आपका समीकरण इस तरह दिखेगा: = १.५/१.
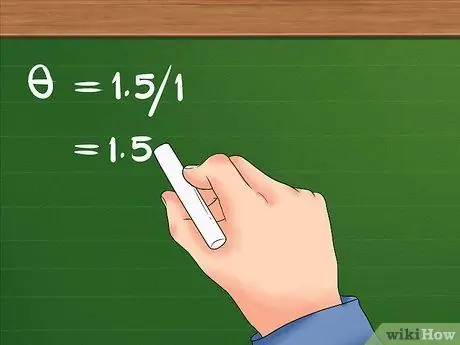
चरण 3. रैखिक विस्थापन को त्रिज्या से विभाजित करें।
इस विभाजन के परिणामस्वरूप वस्तु का कोणीय विस्थापन होगा।
- 1.5 को 1 से विभाजित करने के बाद, परिणाम 1.5 है। लड़की का कोणीय विस्थापन 1.5. है रेडियन
- चूंकि कोणीय विस्थापन मापता है कि कोई वस्तु अपनी प्रारंभिक स्थिति से कितना घूमती है, इसे कोण के रूप में मापा जाना चाहिए, दूरी के रूप में नहीं। रेडियन कोणों को मापने के लिए उपयोग की जाने वाली इकाई है।
5 का भाग 5: प्रवासन के बारे में समझना
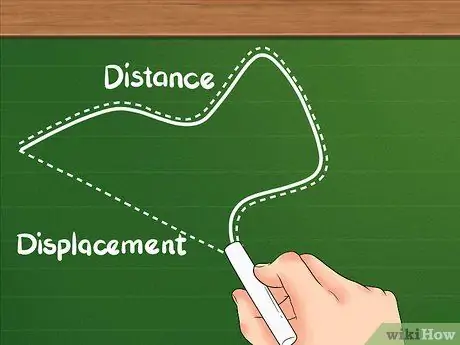
चरण 1. जान लें कि विस्थापन की तुलना में दूरी की एक अलग परिभाषा है।
दूरी दर्शाती है कि वस्तु द्वारा तय की गई कुल दूरी कितनी है।
- दूरी को अक्सर एक अदिश राशि के रूप में जाना जाता है। दूरी वस्तु की दिशा की परवाह किए बिना किसी वस्तु द्वारा तय की गई दूरी को दर्शाती है।
- उदाहरण के लिए, यदि आप 2 कदम पूर्व, 2 कदम दक्षिण, 2 कदम पश्चिम और फिर 2 कदम उत्तर की ओर चलते हैं, तो आप अपनी प्रारंभिक स्थिति में लौट आएंगे। भले ही आप कुल से गुजरे हों दूरी 10 कदम दूर, तुम बस कदम 0 कदम दूर है क्योंकि आपका अंतिम स्थान वही है जो आपका आरंभिक स्थान है (आपका पथ एक बॉक्स जैसा दिखता है)।

चरण 2. समझें कि विस्थापन दो स्थानों के बीच का अंतर है।
विस्थापन दूरी की तरह गति का कुल योग नहीं है; आपके आरंभ और समाप्ति स्थानों के बीच के क्षेत्र पर ध्यान केंद्रित करता है।
- विस्थापन को सदिश राशि कहा जाता है और वस्तु की गति की दिशा पर विचार करके वस्तु की स्थिति में परिवर्तन को दर्शाता है।
- उदाहरण के लिए, आप पूर्व की ओर 5 कदम चलते हैं। यदि आप पश्चिम की ओर 5 कदम पीछे जाते हैं, तो आप अपने मूल स्थान से विपरीत दिशा में आगे बढ़ेंगे। भले ही आपने 10 कदम पूरे कर लिए हों, लेकिन आपकी स्थिति नहीं बदली है; आपका विस्थापन 0 कदम है।

चरण 3. विस्थापन की कल्पना करते समय आगे और पीछे के शब्दों को याद रखें।
विपरीत दिशा में चलने से वस्तु का विस्थापन समाप्त हो जाता है।
एक फ़ुटबॉल कोच की कल्पना करें जो किनारे पर आगे-पीछे हो। जैसे ही उन्होंने खिलाड़ियों पर चिल्लाया, वह कई बार बाएं से दाएं शिफ्ट हुए। यदि आप उसे बाएं से दाएं चलते हुए देखते हैं, तो आप देखते हैं कि उसने कितनी दूरी तय की है। हालाँकि, मान लीजिए कि कोच क्वार्टरबैक से बात करने के लिए रुक जाता है। यदि वह चलने से पहले अपने प्रारंभिक स्थान से भिन्न बिंदु पर है, तो आप प्रशिक्षक की चाल को देख रहे हैं।

चरण 4. जान लें कि विस्थापन को सीधे पथ का उपयोग करके मापा जाता है, न कि वृत्ताकार पथ से।
विस्थापन का पता लगाने के लिए, आपको दो बिंदुओं के बीच अंतर की गणना करने का सबसे छोटा और सबसे कुशल तरीका खोजना होगा।
- एक वृत्ताकार पथ आपको आपके आरंभिक स्थान से आपके अंतिम स्थान तक ले जाएगा, लेकिन यह सबसे छोटा रास्ता नहीं है। इसकी कल्पना करने में आपकी मदद करने के लिए, कल्पना करें कि आप एक सीधी रेखा में चल रहे हैं और आपको एक स्तंभ मिलता है। आप इस स्तंभ को नहीं तोड़ सकते, इसलिए आप इसके चारों ओर जाएं। भले ही आपकी अंतिम स्थिति वही है जैसे कि आप स्तंभ को तोड़ते हैं, आपको उस लक्ष्य तक पहुंचने के लिए अतिरिक्त कदमों की आवश्यकता होगी।
- यद्यपि विस्थापन एक सीधे पथ का प्रतिनिधित्व करता है, यह जान लें कि आप किसी वस्तु के विस्थापन को माप सकते हैं जो है वर्तमान में एक वृत्ताकार पथ में चलते हैं। इस विस्थापन को कोणीय विस्थापन कहा जाता है और इसकी गणना प्रारंभिक स्थान से अंतिम स्थान तक सबसे छोटा रास्ता निकालकर की जा सकती है।

चरण 5. जान लें कि विस्थापन दूरी के विपरीत ऋणात्मक हो सकता है।
यदि आप अपनी प्रारंभिक दिशा के विपरीत दिशा में आगे बढ़ते हुए अंतिम स्थान पर पहुँच जाते हैं, तो आपका विस्थापन ऋणात्मक होता है।
- उदाहरण के लिए, हम पूर्व में ५ कदम चलते हैं और फिर ३ कदम पश्चिम की ओर चलते हैं। भले ही गणना द्वारा आप अपने प्रारंभिक स्थान से 2 कदम आगे बढ़ते हैं, आपका विस्थापन -2 है क्योंकि आप विपरीत दिशा में आगे बढ़ रहे हैं। आपकी दूरी हमेशा सकारात्मक रहेगी क्योंकि आप पीछे की ओर कदमों, किलोमीटर आदि में गिनती नहीं कर सकते।
- ऋणात्मक विस्थापन का अर्थ यह नहीं है कि विस्थापन घटता है। नेगेटिव का सीधा सा मतलब है कि दिशा विपरीत है।

चरण 6. महसूस करें कि कभी-कभी दूरी और विस्थापन समान हो सकते हैं।
यदि आप सीधे 25 कदम चलते हैं और रुक जाते हैं, तो आपके द्वारा यात्रा की जाने वाली दूरी आपके मूल स्थान से विस्थापन के बराबर होगी।
- यह केवल तभी लागू होता है जब आप एक स्थान से अपने प्रारंभिक स्थान से एक सीधी रेखा में चलते हैं। उदाहरण के लिए, आप सैन फ्रांसिस्को, कैलिफ़ोर्निया में रहते हैं, और लास वेगास, नेवादा में एक नई नौकरी प्राप्त करते हैं। आपको अपनी नौकरी के करीब होने के लिए लास वेगास जाना होगा। अगर आप उड़ने वाले हवाई जहाज पर चढ़ते हैं सीधा सैन फ्रांसिस्को से लास वेगास तक, आप समान दूरी और विस्थापन x की यात्रा करेंगे।
- हालाँकि, यदि आप सैन फ्रांसिस्को से लास वेगास तक ड्राइव करते हैं, तो आप दूरी x की यात्रा करेंगे, लेकिन दूरी y की यात्रा करेंगे। चूंकि कार चलाने में आमतौर पर परिवर्तनशील दिशाएँ होती हैं (इस सड़क के पूर्व में, उस सड़क के पश्चिम में), आप दोनों शहरों के बीच की सबसे छोटी दूरी की तुलना में लंबी दूरी की यात्रा करेंगे।







