औसत गति की गणना कैसे करें: 12 कदम (चित्रों के साथ)

2024 लेखक: Jason Gerald | [email protected]. अंतिम बार संशोधित: 2024-02-01 14:13

औसत गति की गणना करने के लिए आपको केवल कुल विस्थापन की आवश्यकता है। या स्थिति का परिवर्तन, और कुल समय। याद रखें कि वेग किसी वस्तु की दिशा और गति की गणना भी करता है, इसलिए अपने उत्तर में एक दिशा शामिल करें, जैसे "उत्तर," "सामने," या "बाएं।" यदि आपकी गति गणना समस्या में निरंतर त्वरण भी शामिल है, तो आप उत्तर को और भी आसान खोजने का एक त्वरित तरीका सीख सकते हैं।

कदम

विधि 1 का 2: विस्थापन और समय के औसत वेग की गणना करना

चरण 1. याद रखें कि वेग में किसी वस्तु की गति और दिशा दोनों शामिल हैं।

वेग उस दर का वर्णन करता है जिस पर किसी वस्तु की स्थिति में परिवर्तन होता है। यह न केवल वस्तु की गति से ही नहीं, बल्कि उसकी दिशा से भी संबंधित है। "100 मीटर प्रति सेकंड दक्षिण की ओर" एक अलग गति मान है "100 मीटर प्रति सेकंड पूर्व की ओर।"

वे मात्राएँ जिनमें दिशा होती है, सदिश राशियाँ कहलाती हैं। चर के ऊपर एक तीर लिखकर इस मात्रा को एक दिशाहीन मात्रा से अलग किया जा सकता है जिसे अदिश राशि कहा जाता है। उदाहरण के लिए, संकेतन v दर का प्रतिनिधित्व करता है, जबकि संकेतन v ^→ गति या गति + दिशा का प्रतिनिधित्व करता है। इस आलेख में प्रयुक्त v अंकन गति का प्रतिनिधित्व करता है।
वैज्ञानिक समस्याओं में, आपको दूरी को व्यक्त करने के लिए मीटर या अन्य मीट्रिक इकाइयों का उपयोग करना चाहिए, जबकि रोजमर्रा के उद्देश्यों के लिए आप अपनी पसंद की किसी भी इकाई का उपयोग कर सकते हैं।

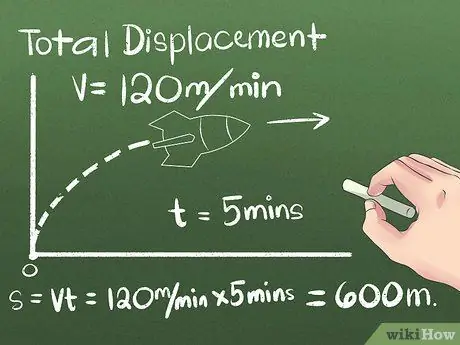
चरण 2. कुल विस्थापन मान ज्ञात कीजिए।

विस्थापन किसी वस्तु की स्थिति में परिवर्तन, या उसके आरंभ और अंत बिंदुओं के बीच की दूरी और दिशा है। वस्तु अपनी अंतिम स्थिति तक पहुँचने से पहले जिस दिशा में चलती है, उसकी उपेक्षा की जा सकती है, क्योंकि केवल प्रारंभ और अंत बिंदुओं के बीच की दूरी को ही ध्यान में रखा जाता है। पहले उदाहरण के लिए, हम एक दिशा में स्थिर गति से गतिमान वस्तु का उपयोग करेंगे:

मान लीजिए कि एक रॉकेट 120 मीटर प्रति मिनट की निरंतर गति से 5 मिनट के लिए उत्तर की ओर बढ़ रहा है। अंतिम स्थिति की गणना करने के लिए, सूत्र s = vt का उपयोग करें, या उसके बाद रॉकेट द्वारा तय की गई दूरी की गणना करने के लिए व्यावहारिक सोच का उपयोग करें (5 मिनट) (120 मीटर/मिनट) = 600 मीटर उत्तर शुरुआती बिंदु से।
निरंतर त्वरण से संबंधित समस्याओं के लिए, आप उन्हें s = vt + at. से हल कर सकते हैं², या उत्तर खोजने के लिए किसी अन्य खंड में वर्णित संक्षिप्त विधि का उपयोग करें।

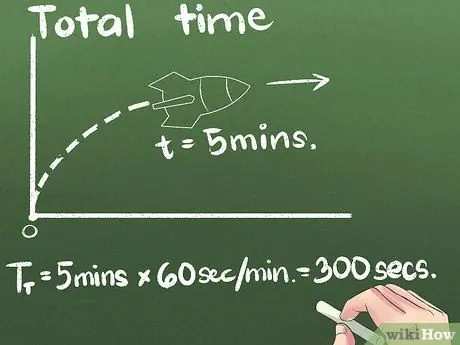
चरण 3. खर्च किए गए कुल समय का पता लगाएं।

हमारे उदाहरण में, रॉकेट 5 मिनट के लिए आगे बढ़ रहा है। आप समय की किसी भी इकाई में औसत गति व्यक्त कर सकते हैं, लेकिन दूसरी अंतरराष्ट्रीय वैज्ञानिक मानक इकाई है। हम इस उदाहरण में सेकंड की इकाइयों को बदल देंगे: (5 मिनट) x (60 सेकंड/मिनट) = ३०० सेकंड.

वैज्ञानिक समस्याओं में भी, यदि प्रश्न घंटे या समय की एक बड़ी इकाई का उपयोग करता है, तो पहले गति की गणना करना आसान होगा, फिर अंतिम उत्तर को मीटर/सेकंड में परिवर्तित करें।

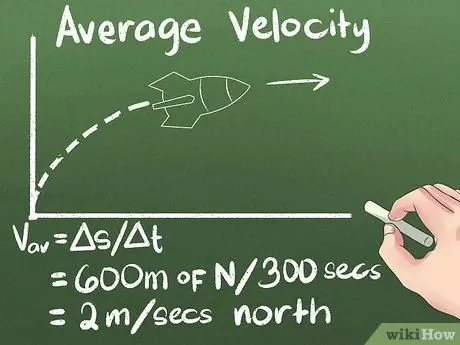
चरण 4. समय के साथ विस्थापन के रूप में औसत वेग की गणना करें।

यदि आप जानते हैं कि कोई वस्तु कितनी दूर चल रही है, और उसे वहां पहुंचने में कितना समय लगेगा, तो आपको पता चल जाएगा कि वह कितनी तेजी से आगे बढ़ रही है। इसलिए हम जिस उदाहरण का उपयोग कर रहे हैं, उसके लिए रॉकेट की औसत गति (600 मीटर उत्तर) / (300 सेकंड) =. है 2 मीटर/सेकंड उत्तर.

एक दिशा शामिल करना याद रखें (जैसे "सामने" या "उत्तर")।
सूत्र में वी_{ए वी} = एस/Δt. डेल्टा प्रतीक का अर्थ है "परिवर्तन," इसलिए s/Δt का अर्थ है "समय की अवधि में स्थिति में परिवर्तन।"
औसत गति को v. के रूप में लिखा जा सकता है_{ए वी}, या इसके ऊपर एक क्षैतिज रेखा के साथ v के रूप में।

चरण 5. अधिक जटिल समस्याओं को हल करें।

यदि कोई वस्तु अपनी दिशा या गति बदलती है, तो भ्रमित न हों। औसत गति अभी भी "केवल" कुल विस्थापन और कुल समय से गणना की जाती है। प्रारंभ और समाप्ति बिंदुओं के बीच क्या होता है जिसे आप अनदेखा कर सकते हैं। समान विस्थापन और कुल समय के साथ यात्रा करने वाली वस्तु के कुछ उदाहरण निम्नलिखित हैं, और इस प्रकार, समान औसत वेग:

एना 2 सेकंड के लिए 1 मीटर/सेकंड की गति से पश्चिम की ओर चलती है, फिर अचानक 3 मीटर/सेकंड की गति से चलती है और 2 सेकंड के लिए पश्चिम की ओर चलती रहती है। कुल विस्थापन है (१ मी/से पश्चिम की ओर)(२ सेकंड) + (३ मीटर/सेकेंड पश्चिम की ओर)(२ सेकंड) = ८ मीटर पश्चिम की ओर। कुल समय 2 सेकंड + 2 सेकंड = 4 सेकंड है। तो औसत गति 8 मीटर पश्चिम / 4 सेकंड =. है 2 मीटर/सेकंड पश्चिम।
बार्ट 3 सेकंड के लिए 5 मीटर/सेकंड की गति से पश्चिम की ओर चलता है, फिर मुड़ता है और 1 सेकंड के लिए 7 मीटर/सेकंड की गति से पूर्व की ओर चलता है। हम पूर्व की ओर गति को "नकारात्मक पश्चिम की ओर गति" के रूप में सोच सकते हैं, इसलिए कुल विस्थापन = (5 मीटर/सेकंड पश्चिम की ओर) (3 सेकंड) + (-7 मीटर/सेकेंड पश्चिम की ओर) (1 सेकंड) = 8 मीटर है। कुल समय = 4 सेकंड। औसत गति = 8 मीटर पश्चिम / 4 सेकंड = 2 मीटर/सेकंड पश्चिम।
शार्लेट उत्तर की ओर 1 मीटर चली और फिर पश्चिम में 8 मीटर चली, फिर दक्षिण में 1 मीटर चली। पूरी यात्रा को पूरा करने में 4 सेकंड का समय लगता है। कागज के एक टुकड़े पर आरेख बनाएं, और आप देखेंगे कि अंत बिंदु प्रारंभिक बिंदु से 8 मीटर पश्चिम में है, इसलिए यह मान विस्थापन है। इसमें लगने वाला कुल समय 4 सेकंड है, इसलिए औसत गति 8 मीटर पश्चिम / 4 सेकंड =. है 2 मीटर/सेकंड पश्चिम।

विधि २ का २: निश्चित त्वरण के औसत वेग की गणना करना

चरण 1. प्रारंभिक वेग और निरंतर त्वरण पर विचार करें।

मान लीजिए कि हमारी समस्या यह है कि "एक साइकिल 5 मीटर/सेकेंड की गति से दाईं ओर बढ़ रही है, जिसमें 2 मीटर/सेकेंड का निरंतर त्वरण है². यदि यह साइकिल 5 सेकंड चलती है, तो इसकी औसत गति क्या है?"

यदि इकाई "मीटर/सेकंड²"आपको भ्रमित करने के लिए, इसे "मीटर/सेकंड/सेकंड" या "मीटर प्रति सेकंड प्रति सेकंड" लिखें।

चरण 2. अंतिम वेग ज्ञात करने के लिए त्वरण का प्रयोग करें।

त्वरण, संकेतन a द्वारा निरूपित, वेग (या दर) के परिवर्तन की दर है। गति में निरंतर वृद्धि की दर से वृद्धि होती है। आप साइकिल यात्रा के दौरान अलग-अलग समय पर गति ज्ञात करने के लिए त्वरण का उपयोग करके एक तालिका बना सकते हैं। समस्या के अंतिम बिंदु (t = 5 सेकंड पर) को खोजने के लिए हमें यह तालिका बनाने की आवश्यकता है, लेकिन हम इस अवधारणा को समझना आपके लिए आसान बनाने के लिए एक लंबी तालिका बनाएंगे:

प्रारंभिक बिंदु (समय t = 0 सेकंड) पर, साइकिल 5 मीटर/सेकेंड की गति से चल रही है।
1 सेकंड (t = 1) के बाद, साइकिल 5 मीटर/सेकंड + पर = 5 मीटर/सेकंड + (2 मीटर/सेकंड) की गति से आगे बढ़ रही है²)(1 सेकंड) = 7 मीटर/सेकंड।
t = 2 पर, साइकिल 5+(2)(2) = 9 मीटर/सेकंड की गति से दाईं ओर जा रही है।
t = 3 पर, साइकिल 5+(2)(3) = 11 मीटर/सेकंड की गति से दाईं ओर बढ़ रही है।
t = 4 पर, साइकिल 5+(2)(4) = 13 मीटर/सेकंड की गति से दाईं ओर बढ़ रही है।
t = 5 पर, साइकिल दायीं ओर 5+(2)(5) =. की गति से चल रही है 15 मीटर/सेकंड.

चरण 3. औसत गति ज्ञात करने के लिए इस सूत्र का उपयोग करें।

यदि और "केवल" यदि त्वरण स्थिर है, तो औसत वेग अंतिम और प्रारंभिक वेगों के योग के औसत मान के बराबर होगा। (वी_एफ +वी_मैं)/2. ऊपर दी गई हमारी उदाहरण समस्या के लिए, साइकिल की प्रारंभिक गति v. है_मैं 5 मीटर/सेकंड। गणना करने के बाद, अंतिम वेग v. है_एफ 15 मीटर/सेकंड। इन दोनों मानों को एक साथ जोड़ने पर, हमें मिलता है (15 मीटर/सेकंड + 5 मीटर/सेकंड)/2 = (20 मीटर/सेकंड)/2 = 10 मीटर/सेकंड सही दिशा.

इस मामले में "सही" दिशा शामिल करना याद रखें।
इस शब्द को v. के रूप में लिखा जा सकता है₀ (समय पर वेग 0, या प्रारंभिक वेग) और v (अंतिम वेग)।

चरण 4. औसत वेग सूत्र को सहजता से समझें।

औसत वेग ज्ञात करने के लिए हम किसी भी बिंदु पर वेग का उपयोग कर सकते हैं और उन सभी का औसत ज्ञात कर सकते हैं। (यह औसत की परिभाषा है।) चूंकि इसके लिए कैलकुलस या अनंत समय की आवश्यकता होती है, इसलिए इस सूत्र को अधिक सहजता से समझें। हर बार लेने के बजाय, दो समय बिंदुओं के औसत वेग की गणना करें और परिणाम देखें। एक बिंदु समय सवारी की शुरुआत के करीब है, जहां बाइक धीरे-धीरे जा रही है, और दूसरा बिंदु अंत बिंदु के पास है जहां बाइक तेजी से जा रही है।

चरण 5. सहज ज्ञान युक्त सिद्धांत का परीक्षण करें।

समय में विभिन्न बिंदुओं पर वेग निर्धारित करने के लिए उपरोक्त तालिका का प्रयोग करें। हमारे मानदंड को पूरा करने वाले कुछ जोड़े हैं (t=0, t=5), (t=1, t=4), या (t=2, t=3)। आप चाहें तो इस फॉर्मूले को पूर्णांकों के अलावा अन्य t मानों के साथ भी परख सकते हैं।

आप जो भी अंक चुनते हैं, उस समय औसत वेग हमेशा समान रहेगा। उदाहरण के लिए, ((5+15)/2), ((7+13)/2), या ((9+11)/2) सभी बराबर 10 मीटर/सेकंड दाईं ओर।

चरण 6. सहज व्याख्या को पूरा करें।

यदि हम प्रत्येक समय की सूची के साथ इस पद्धति का उपयोग करते हैं, तो हम यात्रा के पहले भाग और यात्रा के दूसरे भाग के औसत की गणना करना जारी रखेंगे। प्रत्येक आधे भाग को पूरा करने में लगने वाला समय समान है, इसलिए जब हम गिनती समाप्त करते हैं तो कोई गति नहीं खोती है।

चूँकि दोनों में से कोई भी जोड़ी समान परिणाम देगी, इन गतियों का औसत भी मूल्य में समान होगा। हमारे उदाहरण में, संपूर्ण की गति "10 मीटर/सेकंड दाईं ओर" अभी भी 10 मीटर/सेकंड दाईं ओर होगी।
हम किसी भी जोड़ी के औसत की गणना करके यह मान प्राप्त कर सकते हैं, उदाहरण के लिए प्रारंभिक और अंतिम वेग। हमारे उदाहरण में, ये गति t=0 और t=5 पर पहुंच गई हैं, और ऊपर दिए गए सूत्र का उपयोग करके गणना की जा सकती है: (5+15)/2 = 10 मीटर/सेकंड दाईं ओर।

चरण 7. इस सूत्र को गणितीय रूप से समझें।

यदि आप सूत्रों के रूप में लिखे गए प्रमाणों के साथ अधिक सहज हैं, तो आप निरंतर त्वरण मानकर तय की गई दूरी की गणना करने के लिए एक सूत्र के साथ शुरू कर सकते हैं, और वहां से सूत्र प्राप्त कर सकते हैं:

एस = वी_मैंटी + एटी². (तकनीकी रूप से s और t, या स्थिति में परिवर्तन और समय में परिवर्तन, लेकिन यदि आप s और t लिखते हैं तो आपको भी समझा जाएगा।)
औसत गति वी_{ए वी} s/t के रूप में परिभाषित किया गया है, इसलिए फ़ॉर्मूला को s/t के रूप में दर्ज करें।
वी_{ए वी} = एस/टी = वी_मैं + अत
त्वरण x समय कुल वेग में परिवर्तन के बराबर है, या v_एफ - वी_मैं. तो हम सूत्र में "at" को प्रतिस्थापित कर सकते हैं, और प्राप्त कर सकते हैं:
वी_{ए वी} = वी_मैं + (वी_एफ - वी_मैं).
सरल करें: वी_{ए वी} = वी_मैं + वी_एफ - वी_मैं = वी_मैं + वी_एफ = (वी_एफ +वी_मैं)/2.

टिप्स

वेग गति से भिन्न है क्योंकि वेग एक सदिश राशि है जबकि गति एक अदिश राशि है। सदिश राशियों में दिशा और परिमाण दोनों शामिल होते हैं, जबकि अदिश राशियों में केवल परिमाण शामिल होता है।
यदि वस्तु एक आयाम में घूम रही है, जैसे कि बाएं-दाएं, तो आप एक दिशा (जैसे दाएं) का प्रतिनिधित्व करने के लिए एक सकारात्मक संख्या और दूसरी दिशा (बाएं) का प्रतिनिधित्व करने के लिए एक नकारात्मक संख्या का उपयोग कर सकते हैं। इस अंकन को अपने पृष्ठ के शीर्ष पर लिखें ताकि यह आपके काम को पढ़ने वाले लोगों के लिए स्पष्ट हो।