संख्यात्मक डेटा का तरीका कैसे खोजें: 8 कदम (चित्रों के साथ)

2024 लेखक: Jason Gerald | [email protected]. अंतिम बार संशोधित: 2024-01-15 08:15

आँकड़ों में, बहुलक वह संख्या है जो संख्याओं या डेटा के समूह में सबसे अधिक बार दिखाई देती है। डेटा में हमेशा केवल एक ही मोड नहीं होता है, यह दो या अधिक हो सकता है (इसलिए इसे बिमोडल या मल्टीमॉडल कहा जाता है)। दूसरे शब्दों में, डेटा में सबसे अधिक बार आने वाली सभी संख्याओं को बहुलक कहा जा सकता है। मोड कैसे खोजें, यह जानने के लिए नीचे दिए गए चरणों का पालन करें।

कदम

विधि 1: 2 में से एक डेटा का तरीका ढूँढना

चरण 1. आंकड़ों में संख्याओं को लिखिए।

मोड आमतौर पर सांख्यिकीय डेटा या संख्याओं की सूची से लिया जाता है। तो आपको मोड खोजने के लिए डेटा की आवश्यकता है। यह अनुशंसा की जाती है कि आप पहले डेटा को रिकॉर्ड करें या लिखें, क्योंकि केवल अपने दिमाग में इसे देखकर और विश्लेषण करके मोड ढूंढना काफी मुश्किल है, जब तक कि डेटा बहुत कम न हो। यदि आप कागज और पेंसिल या पेन का उपयोग कर रहे हैं, तो बाद में इसे छाँटने के लिए पहले डेटा को लिख लें। यदि आप कंप्यूटर पर हैं, तो आप उन्हें बाद में स्वचालित रूप से सॉर्ट करने के लिए एक स्प्रेडशीट प्रोग्राम का उपयोग कर सकते हैं।

किसी आँकड़ों का बहुलक ढूँढ़ने की प्रक्रिया को समझना आसान है यदि हम किसी उदाहरण समस्या से उसका अनुसरण करें। अभी के लिए, आइए इस नमूना डेटा का उपयोग करें: {18, 21, 11, 21, 15, 19, 17, 21, 17}. अगले कुछ चरणों में हम बहुलक की खोज करेंगे।

चरण 2. सबसे छोटी से सबसे बड़ी संख्याओं को क्रमबद्ध करें।

डेटा सॉर्ट करना वास्तव में नहीं किया जा सकता है। लेकिन यह कदम वास्तव में आपको बहुलक खोजने में मदद करेगा क्योंकि समान संख्याएं एक दूसरे के बगल में होंगी जिससे गणना करना आसान हो जाएगा। यदि आपके डेटा का आकार बहुत बड़ा है, तो त्रुटि-प्रवण दर को कम करने के लिए यह कदम उठाया जाना चाहिए।

• यदि आप कागज और पेंसिल या पेन का उपयोग कर रहे हैं, तो आपके द्वारा पहले लिखे गए डेटा को क्रम में फिर से लिखें। डेटा से सबसे छोटी संख्या ज्ञात करके प्रारंभ करें। यदि आप इसे पाते हैं, तो इसे एक नई लाइन पर लिखें, फिर पिछली डेटा सूची में संख्या को काट दें। अगली सबसे छोटी संख्या ज्ञात कीजिए और यही कार्य तब तक कीजिए जब तक आप सभी संख्याओं को क्रमित न कर लें।
• यदि आप अपने कंप्यूटर पर स्प्रेडशीट प्रोग्राम का उपयोग करते हैं, तो आप कुछ ही क्लिक में संख्याओं की सूची को क्रमित कर सकते हैं।

• ऊपर दिए गए हमारे उदाहरण में, सॉर्ट किया गया डेटा है {11, 15, 17, 17, 18, 19, 21, 21, 21}.

चरण 3. गिनें कि कोई संख्या कितनी बार प्रकट होती है।

छोटे डेटा के लिए, आप बस उस डेटा को देख सकते हैं जिसे सॉर्ट किया गया है, फिर देखें कि वहां कौन सी संख्या सबसे अधिक दिखाई दे रही है। यदि आपका डेटा बड़ा है, तो आपको त्रुटियों से बचने के लिए एक-एक करके उनकी गणना करनी चाहिए।

• यदि आप कागज और पेंसिल या पेन का उपयोग कर रहे हैं, तो गलत गणना से बचने के लिए ध्यान दें कि प्रत्येक संख्या कितनी बार दिखाई देती है। यदि आप किसी कंप्यूटर पर स्प्रेडशीट का उपयोग करते हैं, तो आप इसे किसी अन्य कॉलम में भी रिकॉर्ड कर सकते हैं, या यदि आप जानते हैं, तो आप प्रोग्राम में दिए गए फ़ार्मुलों का उपयोग कर सकते हैं।
• उदाहरण समस्या में, अर्थात् ({११, १५, १७, १७, १८, १९, २१, २१, २१}), संख्या ११ एक बार आती है, १५ एक बार आती है, १७ दो बार आती है, १८ एक बार आती है, १९ एक बार आती है, तथा 21 तीन बार प्रकट होता है. वहां से, यह स्पष्ट है कि 21 वह संख्या है जो सबसे अधिक बार दिखाई देती है।

चरण 4. सबसे अधिक बार दिखाई देने वाली संख्या डेटा का बहुलक है।

यह नोट करने के बाद कि प्रत्येक एक ही संख्या कितनी बार प्रकट होती है, आपको पहले से ही पता होना चाहिए कौन सी संख्या सबसे अधिक दिखाई देती है, जिसका अर्थ है डेटा मोड. उसे याद रखो यह संभव है कि डेटा में एक से अधिक मोड हों. यदि एक डेटा में दो मोड होते हैं, तो डेटा को बिमोडल कहा जा सकता है, जबकि यदि इसमें तीन मोड होते हैं, तो इसे त्रिमोडल कहा जाता है, और इसी तरह।

• उदाहरण समस्या में, मोड 21. है क्योंकि यह सबसे अधिक बार प्रकट होता है।
• यदि कोई अन्य संख्या है जो तीन बार प्रकट होती है, तो 21 और वह संख्या बहुलक है।

चरण 5. आँकड़ों के बहुलक को उसके माध्य (माध्य) और माध्यिका द्वारा विभेदित करें।

तीन सांख्यिकीय अवधारणाओं पर आमतौर पर एक चर्चा में चर्चा की जाती है। क्योंकि उनके नाम समान हैं और कभी-कभी उनका मूल्य समान होता है, बहुत से लोगों को उन्हें अलग बताना मुश्किल होता है। हालांकि, भले ही डेटा में एक ही मोड, माध्यिका या औसत हो, ध्यान रखें कि वे अलग हैं और अकेले खड़े हैं। नीचे स्पष्टीकरण पढ़ें।

• माध्य जिसका अर्थ है औसत डेटा की संख्या से विभाजित डेटा मानों का योग है। उदाहरण के लिए, उदाहरण समस्या ({11, 15, 17, 17, 18, 19, 21, 21, 21}) में, कुल डेटा 11 + 15 + 17 + 17 + 18 + 19 + 21 + 21 + 21 है। = 160. और क्योंकि डेटा में 9 मान हैं, तो 160/9 = 17.78.

  

• डेटा को सॉर्ट करने के बाद माध्य मध्य मान होता है और डेटा से छोटे और बड़े मानों को अलग करता है। उदाहरण समस्या में, ({11, 15, 17, 17, 18, 19, 21, 21, 21}), माध्यिका है

  चरण 18. क्योंकि संख्या बीच में है, और डेटा में चार संख्याएँ अधिक और चार संख्याएँ 18 से कम हैं। यदि डेटा एक सम संख्या है, तो मध्य में दो संख्याओं के योग की गणना करके और फिर दो से विभाजित करके माध्यिका प्राप्त की जाती है।

  

विधि २ का २: किसी विशेष समस्या में बहुलक ढूँढना

चरण 1. एक डेटा में कोई मोड नहीं होता है यदि डेटा में सभी संख्याओं में समान संख्या में आवृत्तियां होती हैं।

उदाहरण के लिए, यदि सभी संख्याएँ केवल एक बार दिखाई देती हैं, तो डेटा कोई मोड नहीं क्योंकि कोई भी संख्या दूसरे की तुलना में अधिक बार प्रकट नहीं होती है। यदि सभी संख्याएँ दो बार या अधिक दिखाई दें तो भी यही बात लागू होती है।

यदि हम उपरोक्त उदाहरण समस्या में डेटा को {11, 15, 17, 18, 19, 21} में बदलते हैं, जिसका अर्थ है कि सभी नंबर एक बार दिखाई देते हैं, तो डेटा का कोई मोड नहीं होता है, साथ ही यदि डेटा को {11 में बदल दिया जाता है, 11, 15, 15, 17, 17, 18, 18, 19, 19, 21, 21}।

चरण 2. एक गैर-संख्यात्मक डेटा अभी भी इसके मोड जैसे संख्यात्मक डेटा के लिए खोजा जा सकता है।

आमतौर पर डेटा मात्रात्मक या संख्यात्मक रूप में मौजूद होता है, इसलिए इसे कई तरीकों से संसाधित किया जा सकता है। हालांकि, कभी-कभी ऐसी चीजें होती हैं जो संख्याओं के रूप में नहीं होती हैं। हालाँकि, डेटा की इस विधा को अभी भी केवल डेटा (जो कथनों के रूप में हो सकता है) की खोज करके खोजा जा सकता है जो सबसे अधिक बार होता है। लेकिन आप गैर-संख्यात्मक डेटा के लिए माध्य या माध्यिका नहीं खोज सकते।

• उदाहरण के लिए, मान लीजिए कि आप एक जैविक सर्वेक्षण कर रहे हैं, जो यह पता लगाने के लिए है कि आपके क्षेत्र में पेड़ की कौन-सी प्रजाति उगती है। आपको जो डेटा मिलता है वह है {फायर, मैंगो, स्प्रूस, पाम, स्प्रूस, फ़िर, मैंगो, मैंगो, पाम, फ़िर}। ऐसे डेटा को नाममात्र डेटा कहा जाता है क्योंकि प्रत्येक डेटा मान एक नाम से अलग होता है। इस उदाहरण के लिए, बहुलक है देवदार क्योंकि यह सबसे अधिक बार (पांच बार) प्रकट होता है।
• यदि आप उदाहरण को देखें, तो आप माध्य या माध्यिका की गणना करने का कोई तरीका नहीं है।

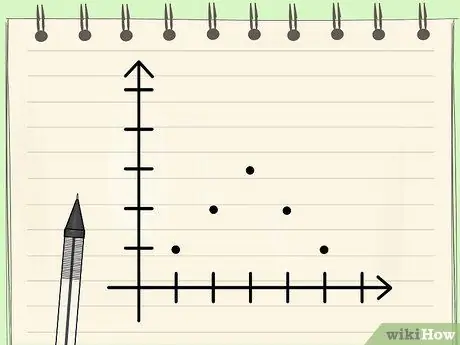
चरण 3. जान लें कि सममित एकरूपी डेटा वितरण के लिए, डेटा का बहुलक, माध्यिका और माध्य समान होगा।

जैसा कि पहले उल्लेख किया गया है, ऐसे समय होंगे जब डेटा सेट का माध्य, माध्यिका और मोड समान होगा। शर्तों में से एक यह है कि यदि डेटा में मूल्यों का कड़ाई से सममित वितरण होता है (जो कि यदि ग्राफिकल रूप में खींचा जाता है तो एक गाऊसी घंटी के आकार का वक्र बन जाएगा)। क्योंकि वितरण सममित है, इस तरह डेटा का तरीका स्वचालित रूप से बीच में डेटा है, क्योंकि यह वह डेटा होना चाहिए जो सबसे अधिक बार दिखाई देता है, और क्योंकि यह मध्य मान है, इसका मतलब है कि संख्या भी औसत है. और यदि आप गणित करते हैं, तो माध्य समान संख्या प्राप्त करेगा।

• उदाहरण के लिए, डेटा {1, 2, 2, 3, 3, 3, 4, 4, 5} से, यदि आप ग्राफ खींचते हैं, तो आपको एक परवलय का ग्राफ प्राप्त होगा। डेटा मोड 3. है क्योंकि यह अक्सर दिखाई देता है, माध्यिका 3. है क्योंकि संख्या बीच में है, और माध्य 1 + 2 + 2 + 3 + 3 + 3 + 4 + 4 + 5 = 27/9 = 3. है.
• इस तरह के मामलों में अपवाद होते हैं, अर्थात् जब इस सममित डेटा में एक से अधिक मोड होते हैं। यदि ऐसा है, क्योंकि माध्य और माध्यिका एक से अधिक मान नहीं हो सकते हैं, तो बहुलक माध्य और माध्यिका के समान नहीं होगा।

टिप्स

• एक डेटा में एक से अधिक मोड हो सकते हैं
• यदि किसी डेटा में सभी संख्याओं के आने की संख्या समान है, तो डेटा मोड मौजूद नहीं है।