आप सोच सकते हैं कि पूर्णांक केवल साधारण संख्याएँ हैं, जैसे 3, -12, 17, 0, 7000, या -582। पूर्णांकों को पूर्ण संख्याएँ भी कहा जाता है क्योंकि वे भिन्न और दशमलव जैसे भागों में विभाजित नहीं होती हैं। पूर्णांकों को जोड़ने और घटाने के बारे में आपको जो कुछ भी चाहिए उसे जानने के लिए इस लेख को पढ़ें, या सीधे उस अनुभाग को पढ़ें जिसकी आपको आवश्यकता है।
कदम
5 में से विधि 1 संख्या रेखा का उपयोग करके धनात्मक पूर्णांकों को जोड़ना और घटाना

चरण 1. संख्या रेखा के बारे में समझें।
संख्या रेखाएँ बुनियादी गणित को कुछ मूर्त और भौतिक में बदल देती हैं जिसे आप देख सकते हैं। केवल कुछ संकेतों और सामान्य ज्ञान के साथ, हम संख्याओं को जोड़ने और घटाने के लिए कैलकुलेटर की तरह इसका उपयोग कर सकते हैं।

चरण 2. आधार संख्या रेखा खींचिए।
कल्पना कीजिए या एक सीधी रेखा खींचिए। अपनी लाइन के बीच में एक डॉट बनाएं। लिखना 0 या इस अवधि के आगे शून्य।
आपकी गणित की किताब इसे शुरुआती बिंदु कह सकती है क्योंकि यह सभी नंबरों के लिए शुरुआती बिंदु है।

चरण 3. अपने शून्य के दाईं और बाईं ओर दो बिंदु बनाएं।
लिखना - 1 बाईं ओर बिंदु के बगल में और
चरण 1। डॉट के बगल में दाईं ओर। यह शून्य के सबसे निकट का पूर्णांक है।
- बिंदुओं के बीच की दूरी को बिल्कुल समान बनाने के बारे में चिंता न करें - जब तक आप जानते हैं कि प्रत्येक बिंदु का क्या अर्थ है, एक संख्या रेखा का उपयोग किया जा सकता है।
- बाईं ओर वाक्य की शुरुआत है।

चरण 4. अधिक संख्याएँ जोड़कर अपनी संख्या रेखा को पूरा करें।
बाईं ओर -1 से अधिक और दाईं ओर 1 से अधिक बिंदु बनाएं। बाईं ओर, -1 से, अपने बिंदुओं को चिह्नित करें - 2, - 3, तथा - 4. दाईं ओर, 1 से अपना बिंदु चिह्नित करें
चरण 2।
चरण 3।, दा
चरण 4।. यदि आपके पास अपने पेपर पर जगह है तो आप जारी रख सकते हैं।
चित्र में उदाहरण -6 से 6 तक की संख्या रेखा को दर्शाता है।

चरण 5. धनात्मक और ऋणात्मक पूर्णांकों के बारे में समझें।
धनात्मक पूर्णांक, जिन्हें भी कहा जाता है प्राकृतिक संख्या, शून्य से बड़ा एक पूर्णांक है। 1, 2, 3, 25, 99 और 2007 धनात्मक पूर्णांक हैं। ऋणात्मक पूर्णांक वे पूर्णांक होते हैं जो शून्य से कम होते हैं (जैसे -2, -4, और -88)।
पूर्णांक पूर्ण संख्याओं पर कॉल करने का एक और तरीका है। 1/2 (आधा) जैसे अंश केवल संख्या का हिस्सा हैं, इसलिए वे पूर्णांक नहीं हैं। दशमलव के समान, उदाहरण के लिए 0.25 (शून्य दशमलव दो पाँच); दशमलव एक पूर्णांक नहीं है।

चरण 6. अपनी उंगली को बिंदु 1 पर रखकर 1+2 हल करना प्रारंभ करें।
हम सरल जोड़ समस्याओं का समाधान करेंगे 1+2 आपके द्वारा अभी बनाई गई संख्या रेखा का उपयोग करना। पहला नंबर है
चरण 1।, इसलिए नंबर पर अपनी उंगली डालना शुरू करें।
-
क्या यह प्रश्न बहुत आसान है?
यदि आपने कभी जोड़ा है, तो आप शायद 1+2 का उत्तर जानते हैं। अच्छा: यदि आप परिणाम जानते हैं, तो यह समझना आसान होगा कि संख्या रेखा कैसे काम करती है। फिर, आप अधिक कठिन जोड़ समस्याओं को हल करने के लिए संख्या रेखा का उपयोग कर सकते हैं या बीजगणित जैसे अधिक कठिन गणित की तैयारी कर सकते हैं।

चरण 7. अपनी उंगली 2 बिंदुओं को दाईं ओर ले जाकर 1+2 जोड़ें।
अपनी उंगली को दाईं ओर स्लाइड करें, आपके द्वारा पास किए जाने वाले बिंदुओं (दूसरी संख्या) की संख्या गिनते हुए। यदि आपने 2 नए अंक पारित किए हैं, तो रुकें। आपकी उंगली जिस नंबर की ओर इशारा कर रही है, वह उत्तर है,
चरण 3।
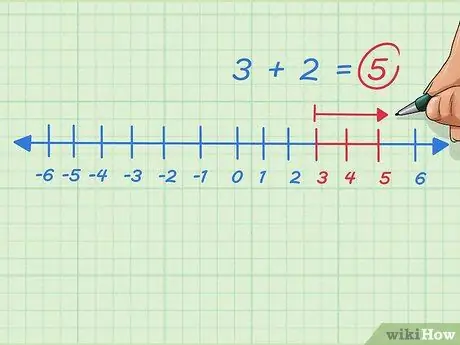
चरण 8. संख्या रेखा पर दाईं ओर जाकर कोई भी धनात्मक पूर्णांक जोड़ें।
मान लीजिए हम 3+2 हल करना चाहते हैं। 3 से प्रारंभ करें, दाईं ओर जाएं या 2 बिंदु जोड़ें। हम 5 पर रुकते हैं। समस्या 3 + 2 = 5 लिखी गई है।

चरण 9. संख्या रेखा पर बाईं ओर जाकर धनात्मक पूर्णांकों को घटाएं।
उदाहरण के लिए, हम 6 -4 को हल करना चाहते हैं, हम 6 से शुरू करते हैं, बाएं 4 बिंदुओं पर जाते हैं, और 2 पर रुकते हैं। यह समस्या 6 - 4 = 2 लिखी गई है।
विधि 2 का 5: संख्या रेखा का उपयोग करके ऋणात्मक संख्याओं को जोड़ना और घटाना

चरण 1. संख्या रेखाओं के बारे में जानें।
यदि आप नहीं जानते कि संख्या रेखा कैसे बनाई जाती है, तो संख्या रेखाओं का उपयोग करके धनात्मक संख्याओं को जोड़ना और घटाना अनुभाग पर वापस जाएँ और जानें कि एक संख्या रेखा कैसे बनाई जाती है।
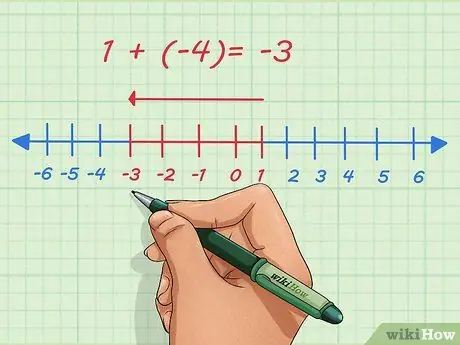
चरण 2. ऋणात्मक संख्याओं के बारे में समझें।
संख्या रेखा पर दाईं ओर की दिशा से धनात्मक संख्याओं का संकेत मिलता है। ऋणात्मक संख्याएँ संख्या रेखा पर बाईं ओर इंगित की जाती हैं। ऋणात्मक संख्याओं को जोड़ने का अर्थ है संख्या रेखा पर बिंदु को बाईं ओर ले जाना।
-
उदाहरण के लिए, आइए 1 और -4 जोड़ें। आमतौर पर, यह प्रश्न इस प्रकार लिखा जाता है:
1 + (-4)
. संख्या रेखा पर, हम 1 से शुरू करते हैं, 4 बिंदुओं को बाईं ओर ले जाते हैं और -3 पर रुकते हैं।
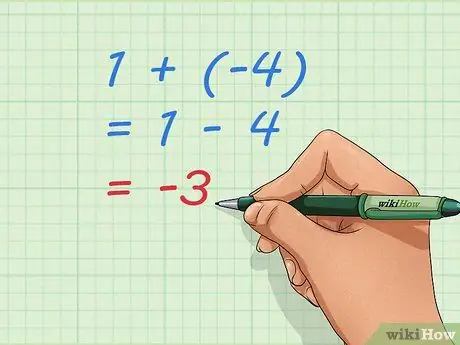
चरण 3. ऋणात्मक संख्याओं के योग को समझने के लिए बुनियादी समीकरणों का उपयोग करें।
ध्यान दें कि -3, हमारा उत्तर, वह संख्या है जो हमें 1 - 4 करने पर प्राप्त होगी। 1 + (-4) जोड़ना और 1 से 4 घटाना एक ही समस्या है। हम इसे एक समीकरण के रूप में लिख सकते हैं, एक गणितीय वाक्य जो समानता दर्शाता है: 1 + (-4) = 1 - 4 = -3
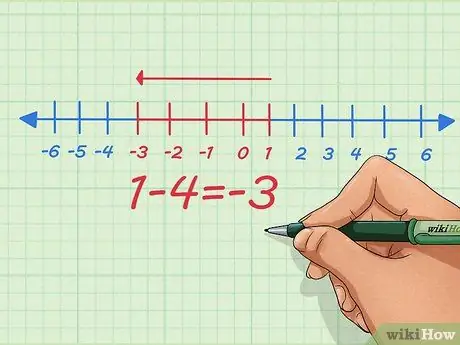
चरण 4। ऋणात्मक संख्याओं को जोड़ने के बजाय, इसे सकारात्मक संख्याओं का उपयोग करके घटाव समस्या में बदल दें।
जैसा कि हम ऊपर दिए गए सरल समीकरण से देख सकते हैं, हम दोनों कर सकते हैं - ऋणात्मक संख्याओं के योग को सकारात्मक संख्याओं के घटाव में बदल दें और इसके विपरीत। हो सकता है कि आपको बिना जाने क्यों नकारात्मक को नकारात्मक में बदलना सिखाया गया हो - यहाँ पर क्यों।
-
उदाहरण के लिए, -4। जब हम -4 और 1 जोड़ते हैं, तो हम 1 को 4 से घटाते हैं। इसे गणित में लिखकर लिखा जा सकता है
1 + (-4) = 1 - 4
. हम इसे संख्या रेखा पर लिख सकते हैं, अपने शुरुआती बिंदु 1 से शुरू करके, फिर बाईं ओर 4 बिंदु जोड़ सकते हैं (दूसरे शब्दों में, -4 जोड़कर)। चूँकि यह एक समीकरण है, एक चीज़ दूसरी चीज़ के बराबर है - इसलिए इसका विपरीत भी सत्य है
1 - 4 = 1 + (-4)
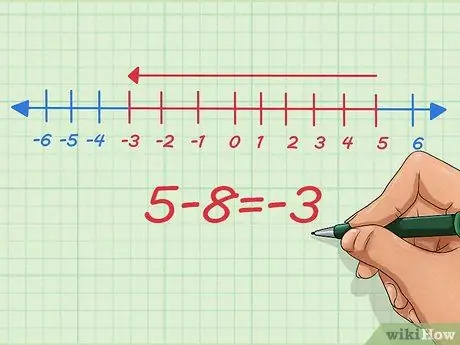
चरण 5. समझें कि किसी संख्या रेखा पर ऋणात्मक संख्याओं को कैसे घटाया जाता है।
संख्या रेखा पर ऋणात्मक संख्याओं को घटाना लंबाई घटाने के समान है। आइए 5 - 8 से शुरू करें।
संख्या रेखा पर, हम अपने शुरुआती बिंदु से 5 से शुरू करते हैं, 8 घटाते हैं, और -3 पर रुकते हैं।
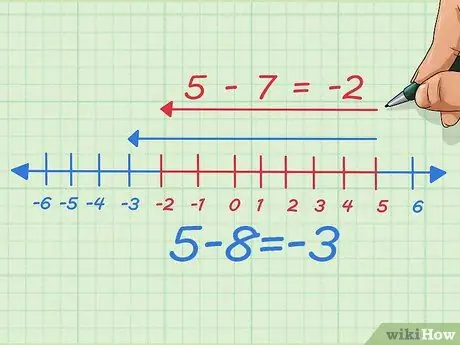
चरण 6. जो राशि आप घटा रहे हैं उसे घटाएं और देखें कि क्या होता है।
मान लीजिए हम एक घटाते हैं, जिस संख्या को हम घटाते हैं, या दूसरे शब्दों में 8 के बजाय 7 घटाते हैं। अब हम संख्या रेखा पर बाईं ओर एक बिंदु घटाते हैं। लिखित रूप में, हमने 5 - 8 = -3 से शुरू किया था अब, हम केवल 7 को बाईं ओर ले जाते हैं, इसलिए यह 5 - 7 = -2 हो जाता है
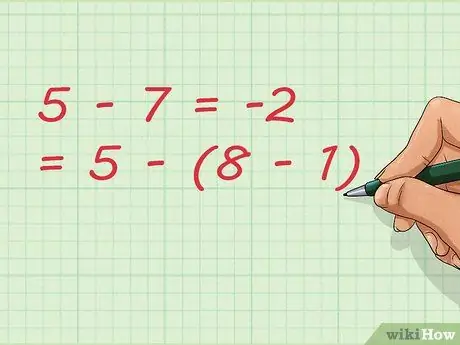
चरण 7. ध्यान दें कि घटाना अतिरिक्त परिणाम दे सकता है।
हमारे उदाहरण में, हम संख्या 1 घटा रहे हैं। समीकरण लिखने में, हम इसे छोटा लिख सकते हैं जैसे: 5 - 7 = -2 = 5 - (8 - 1)

चरण 8. ऋणात्मक संख्याओं को जोड़ते समय ऋणात्मक चिह्नों को धनात्मक में बदलें।
सभी घटावों को जोड़ में बदलने के चरण का उपयोग करके, हम छोटे घटाव लिख सकते हैं जैसे: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
हम पहले से ही जानते हैं कि 5 - 8 = -3, इसलिए समीकरण में से 5 - 8 लें और -3 दर्ज करें:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
हम पहले से ही जानते हैं कि 5 - (8 - 1) है - 5 - 8 में से एक बिंदु घटाता है। हमारा समीकरण यह दिखा सकता है कि 5 - 8 बराबर -3 है, और एक बिंदु घटाने पर -2 मिलता है। समीकरण इस तरह लिखा जा सकता है:
-3 - (-1) = -3 + 1
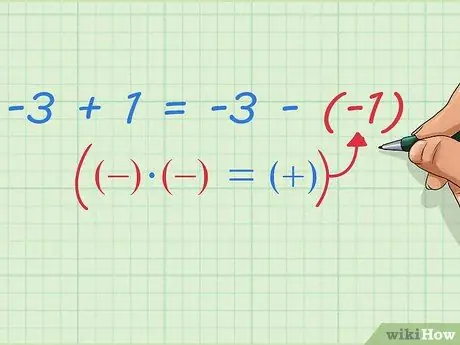
चरण 9. ऋणात्मक संख्याओं के घटाव को योग के रूप में लिखिए।
ध्यान दें कि इसके बाद क्या होता है - हमने पहले ही यह साबित कर दिया है कि: -3 + 1 = -3 - (-1) हम इसे सरल और अधिक सामान्य गणित लेखन नियमों के साथ लिख सकते हैं: पहली संख्या जमा दूसरी संख्या = पहली संख्या घटा (ऋणात्मक दूसरी संख्या) या, एक आसान तरीका जो आपने शायद गणित की कक्षा में सुना होगा: दो नकारात्मक संकेतों को सकारात्मक संकेत में बदलें.
विधि 3 में से 5: धनात्मक बड़े पूर्णांक जोड़ना

चरण 1. 2,503 + 7,461 की योग समस्या को एक संख्या से दूसरी संख्या के ऊपर लिखिए।
संख्याओं को बड़े कॉलम में इस प्रकार लिखें कि 2, 7 से अधिक हो, 5, 4 से अधिक हो, इत्यादि। इस तरह, हम सीखेंगे कि ऐसे पूर्णांकों को कैसे जोड़ा जाए जो संख्या रेखा की कल्पना करने या उपयोग करने के लिए बहुत बड़े हों।
नीचे दी गई संख्या और उसके नीचे की रेखा के बाईं ओर एक + चिह्न लिखें, जैसा कि आप छोटी जोड़ समस्याओं के लिए सीख सकते हैं।
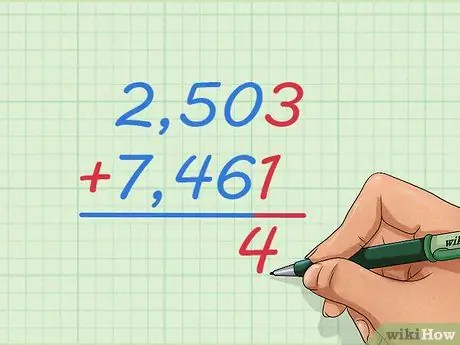
चरण 2. सबसे दाईं ओर दो संख्याओं को जोड़कर प्रारंभ करें।
दाएं से शुरू करना थोड़ा अजीब हो सकता है क्योंकि हम बाएं से नंबर पढ़ते हैं। सही उत्तर पाने के लिए हमें दाईं ओर से जोड़ना होगा, जिसे आप बाद में देख सकते हैं।
-
दो सबसे दाहिने नंबरों के तहत,
चरण 3। दास
चरण 1।, दोनों का योग लिखिए
चरण 4।.

चरण 3. कॉलम में प्रत्येक संख्या को इसी तरह जोड़ें।
बाईं ओर ले जाएं, जोड़ें 0+6, 5+4, तथा 2+7. प्रत्येक युग्म के नीचे उत्तर लिखिए।
आपका उत्तर होना चाहिए: 9.964. यदि आप कोई गलती करते हैं तो अपने काम की जाँच करें।

चरण 4. अब 857+135 जोड़ें।
जैसे ही आप दाईं ओर संख्याओं की पहली जोड़ी जोड़ते हैं, आपको कुछ अलग दिखाई देगा। 7+5 12 के बराबर है, एक दो अंकों की संख्या, लेकिन आप उस कॉलम के नीचे केवल एक अंक लिख सकते हैं। यह जानने के लिए पढ़ते रहें कि आपको क्या करना चाहिए और क्यों आपको हमेशा दाएं से शुरू करना चाहिए न कि बाएं से।

चरण 5. 7+5 जोड़ें और जानें कि उत्तर कहां लिखना है।
7+5=12, लेकिन आप 1 और 2 को लाइन के नीचे नहीं रख सकते। लेकिन, अंतिम अंक लिखिए, चरण 2।, लाइन के नीचे और पहला अंक लिखिए
चरण 1।, स्तंभ के ऊपर बाईं ओर, 5+3.
-
यदि आप इस बारे में उत्सुक हैं कि यह कैसे काम करता है, तो सोचें कि 1 और 2 को विभाजित करने का क्या अर्थ है। आप वास्तव में 12 को. में विभाजित कर रहे हैं
चरण 10. दास
चरण 2।. आप चाहें तो संख्या के ऊपर 10 लिख सकते हैं, और आपको पहले की तरह ही कॉलम 5 और 3 में 1 दिखाई देगा।

चरण 6. उत्तर का अगला अंक प्राप्त करने के लिए 1+5+3 जोड़ें।
अब आपके पास जोड़ने के लिए तीन अंक हैं क्योंकि आपने इस कॉलम में 1 जोड़ा है। उत्तर है
चरण 9., तो आपका उत्तर बन जाता है 92.
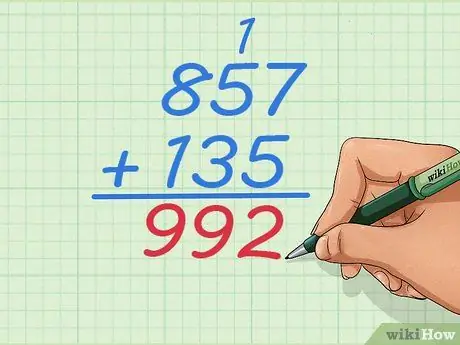
चरण 7. हमेशा की तरह समस्या को पूरा करें।
बाईं ओर के अंकों को तब तक काम करते रहें जब तक कि आप सभी संख्याओं को जोड़ न दें, इस स्थिति में, केवल एक कॉलम बचा है। आपका अंतिम उत्तर होना चाहिए 992.
- आप अधिक जटिल प्रश्नों का प्रयास कर सकते हैं, जैसे 974+568। याद रखें, जब भी आपको दो अंकों की संख्या मिले, तो केवल अंतिम अंक को उत्तर के रूप में लिखें और दूसरे अंक को कॉलम के ऊपर बाईं ओर रखें, जिसे आप आगे जोड़ देंगे। यदि अंतिम कॉलम (दूर बाएं) के उत्तर में दो अंक हैं, तो इसे अपने उत्तर के रूप में लिखें।
- प्रश्नों को हल करने का प्रयास करने के बाद 974+568 प्रश्नों के उत्तर के लिए युक्तियाँ अनुभाग देखें।
विधि 4 में से 5: धनात्मक बड़े पूर्णांकों को घटाना

चरण 1. घटाव समस्या 4.713 - 502 को दूसरी संख्या के ऊपर पहली संख्या के साथ लिखें।
इसे इस प्रकार लिखें कि 3 सीधे 2 से ऊपर हो, 1 0 से ऊपर हो, 7 5 से ऊपर हो, और 4 रिक्त स्थान के ऊपर हो।
आप 4 के नीचे 0 लिख सकते हैं यदि इससे आपको यह याद रखने में मदद मिलती है कि कौन सी संख्या किस संख्या से ऊपर है। आप किसी संख्या को बदले बिना उसके सामने हमेशा 0 जोड़ सकते हैं। इसे संख्या से पहले जोड़ना सुनिश्चित करें, इसके बाद नहीं।

चरण 2. नीचे दी गई प्रत्येक संख्या को उसके ठीक ऊपर वाली संख्या से घटाएं।
हमेशा दाएं से शुरू करें। 3-2, 1-0, 7-5 और 4-0 को हल करें, प्रत्येक प्रश्न का उत्तर दो घटाई गई संख्याओं के ठीक नीचे लिखें।
परिणाम है, 4.211.

चरण 3. अब इसी तरह प्रश्न 924 - 518 लिखें।
इन संख्याओं में अंकों की संख्या समान होती है, इसलिए आप इन्हें आसानी से लिख सकते हैं। यदि आप इसे पहले से नहीं जानते हैं तो यह समस्या आपको पूर्णांकों को घटाने के बारे में कुछ सिखाएगी।

चरण 4. पहली समस्या को हल करना सीखें, जो सबसे दाईं ओर है।
4 - 8. यह समस्या जटिल है क्योंकि 4 8 से कम है, लेकिन ऋणात्मक संख्याओं का उपयोग न करें, लेकिन इन चरणों का पालन करें:
- ऊपर की पंक्ति में, 2 को क्रॉस करें और 1 लिखें। 2 4 के बाईं ओर होना चाहिए।
- 4 को क्रॉस करें और 14 लिखें। इसे एक संकीर्ण जगह में करें ताकि यह स्पष्ट हो कि 14, 8 से अधिक है। पर्याप्त जगह होने पर आप 14 बनाने के लिए 4 के सामने 1 भी लिख सकते हैं।
- आपने अभी-अभी जो किया है वह दहाई के स्थान से 1 उधार लें या दाएँ से दूसरा स्तंभ लें और इसे इकाई के स्थान या सबसे दाएँ स्तंभ में 10 में बदलें। एक बार संख्या 10, संख्या 1 के दस गुना के बराबर है, तो यह वही है।

चरण 5. अब प्रश्न 14 - 8 को हल करें और सबसे दाहिने कॉलम के नीचे उत्तर लिखें।
इसे सबसे दाईं उत्तर पंक्ति पर 6 लिखा होना चाहिए था।

चरण 6. आपके द्वारा लिखे गए नए नंबर का उपयोग करके, बाईं ओर अगला कॉलम पूरा करें।
घटाव 1 - 1 होना चाहिए, जो 0 के बराबर है।
आपका उत्तर अब होना चाहिए 06.

चरण 7. अंतिम घटाव, सबसे बाएं कॉलम को पूरा करके समस्या को हल करें।
९ – ५ = ४, अतः आपका अंतिम उत्तर है 406.

चरण 8. अब हम छोटी संख्याओं में से बड़ी संख्याओं को घटाने की समस्या को हल करते हैं।
मान लीजिए आपको 415,990 - 968,772 पूरा करने के लिए कहा जाता है। पहले नंबर के नीचे दूसरा नंबर लिखें और आपको पता चलेगा कि नीचे दी गई संख्या बड़ी है! आप बाईं ओर के पहले अंक से तुरंत बता सकते हैं: 9 4 से बड़ा है, इसलिए 9 से शुरू होने वाली संख्याएं बड़ी हैं।
सुनिश्चित करें कि आपने तुलना करने से पहले कॉलम को सही ढंग से लिखा है। 912 नहीं 5000 से अधिक आप बता सकते हैं कि क्या आप कॉलम को सही ढंग से लिखते हैं क्योंकि 5 के नीचे कोई संख्या नहीं है। आप शून्य सहायता जोड़ सकते हैं, उदाहरण के लिए, 912 को 0912 के साथ लिखें ताकि कॉलम 5000 के बराबर हो।

चरण 9. बड़ी संख्या के नीचे छोटी संख्या लिखिए और उत्तर के सामने - चिन्ह लगाइए।
जब भी आप किसी संख्या को छोटी संख्या से घटाते हैं, तो परिणाम एक ऋणात्मक संख्या होती है। इस चिन्ह को घटाने से पहले लिखना बेहतर है ताकि आप इसे लिखना न भूलें।

चरण 10. उत्तर देने के लिए, बड़ी संख्या में से छोटी संख्या घटाएं और - चिह्न लिखना न भूलें।
आपका उत्तर नकारात्मक होगा, जो कि - चिन्ह से प्रदर्शित होता है। नहीं एक छोटी संख्या में से एक बड़ी संख्या को घटाने का प्रयास करता है, फिर परिणाम को ऋणात्मक बनाता है; आपका उत्तर गलत होगा।
हल करने के लिए नई समस्या है: 968,772 - 415,990 = -? इस समस्या को हल करने का प्रयास करने के बाद उत्तर के लिए युक्तियाँ अनुभाग देखें।
विधि 5 का 5: ऋणात्मक पूर्णांकों को जोड़ना और घटाना
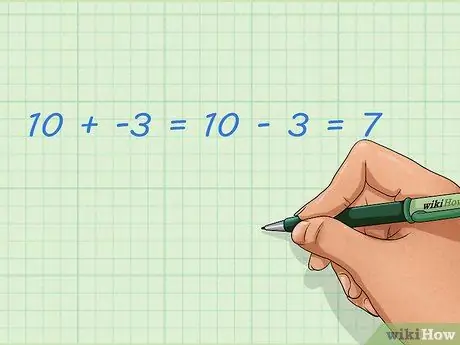
चरण 1. ऋणात्मक और धनात्मक संख्याओं को जोड़ना सीखें।
ऋणात्मक पूर्णांकों को जोड़ना धनात्मक पूर्णांकों को घटाने के समान है। दूसरे खंड में वर्णित संख्या रेखा के साथ ऐसा करना आसान है, लेकिन आप इसे शब्दों में भी सोच सकते हैं। ऋणात्मक संख्याएँ साधारण संख्याएँ नहीं हैं; यह संख्या शून्य से कम है और ली गई राशि का प्रतिनिधित्व कर सकती है। यदि आप इसे नियमित संख्या में जोड़ते हैं, तो परिणाम छोटा हो जाता है।
- उदाहरण: १० + -3 = १० - ३ = ७
- उदाहरण: -12 + 18 = 18 + -12 = 18 - 12 = 6. याद रखें कि आप हमेशा संख्याओं के क्रम को जोड़ में बदल सकते हैं, लेकिन घटाव में नहीं।
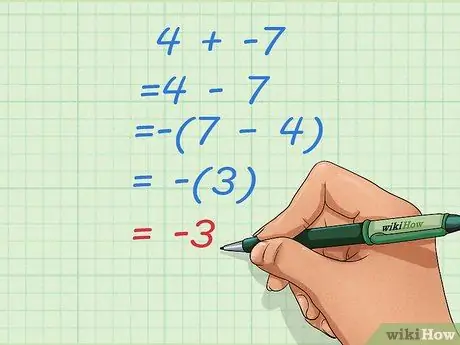
चरण २। जानें कि यदि आप इसे छोटी प्रारंभिक संख्या के साथ घटाव समस्या में बदल देते हैं तो आपको क्या करना होगा।
कभी-कभी, ऊपर दिए गए जैसे घटाव की समस्याओं में परिवर्तन करने से 4 - 7 जैसे विषम उत्तर हो सकते हैं। जब ऐसा होता है, तो संख्याओं के क्रम को उलट दें और अपना परिणाम नकारात्मक बना दें।
- मान लें कि आपकी प्रारंभिक समस्या 4 + -7 है।
- इसे घटाव की समस्या में बदलें: 4 - 7
- क्रम को उल्टा करें और परिणाम को नकारात्मक बनाएं: -(7 - 4) = -(3) = -3।
- यदि आप समीकरणों में कोष्ठकों का उपयोग करने से परिचित नहीं हैं, तो इस बारे में सोचें: 4 - 7 ऋणात्मक चिह्न के जोड़ के साथ 7 - 4 में बदल जाता है। 7 - 4 = 3, लेकिन हमें इसे -3 में बदलना होगा ताकि प्रश्नों 4 - 7 का उत्तर सही हो।
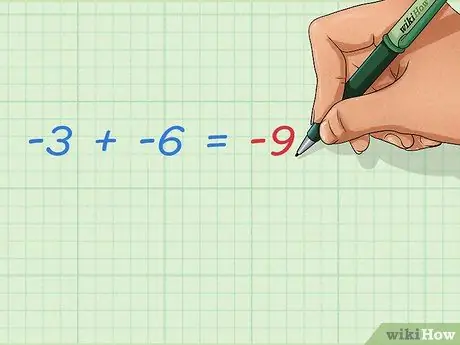
चरण 3. दो ऋणात्मक पूर्णांकों को जोड़ना सीखें।
जोड़े गए दो ऋणात्मक अंक हमेशा ऋणात्मक परिणाम को बड़ा बनाते हैं। चूंकि कोई सकारात्मक संख्या नहीं जोड़ी गई है, परिणाम 0 से और दूर होगा। उत्तर आसान है:
- -3 + -6 = -9
- -15 + -5 = -20
- क्या आप पैटर्न देखते हैं? आपको केवल संख्याओं को ऐसे जोड़ना है जैसे कि वे धनात्मक संख्याएँ हों और एक ऋणात्मक चिह्न जोड़ें। -4 + -3 = -(4 + 3) = -7
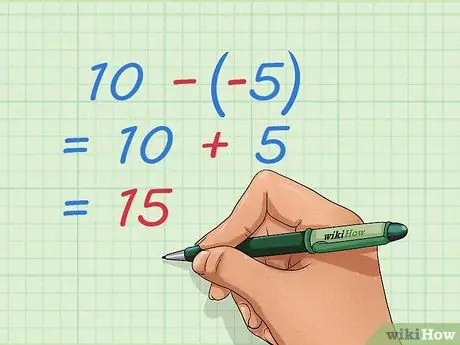
चरण 4. ऋणात्मक पूर्णांकों को घटाना सीखें।
जोड़ समस्या की तरह, आप समस्या को फिर से लिख सकते हैं ताकि आपके पास केवल सकारात्मक संख्याएँ हों। यदि आप ऋणात्मक संख्याओं को घटाते हैं, तो आप पहले से ली गई कुछ चीजों को हटा देते हैं, जो सकारात्मक संख्याओं को जोड़ने के समान है।
- नकारात्मक संख्याओं को चोरी का धन समझें। अगर आप चुराए गए पैसे को घटाते या निकालते हैं ताकि आप उसे वापस कर सकें, यह किसी को पैसे देने जैसा है, है ना?
- उदाहरण: १० - -5 = १० + ५ = १५
- उदाहरण: -1 - -2 = -1 + 2. आप पहले ही चरण में इस समस्या को हल करना सीख चुके हैं, याद रखें? यदि आप भूल गए हैं तो ऋणात्मक और धनात्मक संख्याओं को जोड़ने का तरीका फिर से पढ़ें।
- यहां पिछले उदाहरण का पूरा समाधान दिया गया है: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1।
टिप्स
- आप जहां रहते हैं उसके आधार पर आपने (.) के बजाय अल्पविराम (,) का उपयोग करके 2,521,301 जैसी लंबी संख्याएं लिखी होंगी। आपका शिक्षक आपसे जो माँगता है उसका उपयोग करें ताकि आप अन्य लेखन प्रणालियों के साथ भ्रमित न हों।
- विभिन्न संख्याओं को दर्शाने के लिए विभिन्न पैमानों पर अपनी संख्या रेखाएँ खींचिए। ऐसा कोई नियम नहीं है कि संख्या रेखा पर प्रत्येक दूरी 1 के बराबर होती है। एक संख्या रेखा की कल्पना करें जो 1 के बजाय 10 हो। इस तथ्य के अलावा कि प्रत्येक बिंदु अब 10 है, जोड़ और घटाव समान रहते हैं। विश्वास न हो तो आजमा कर देखिये।
- यदि आप लंबी संख्या वाले खंड में विशेष चुनौती वाले प्रश्नों का प्रयास करते हैं, तो यहां उत्तर दिया गया है: 974 + 568 = 1.542. 415,990 – 968,772 से उत्तर है - 552.782.







