भिन्नों को जोड़ना और घटाना एक महत्वपूर्ण कौशल है। रोजमर्रा की जिंदगी में हर समय भिन्न दिखाई देते हैं, खासकर गणित की कक्षाओं में, प्राथमिक से लेकर कॉलेज तक। समतुल्य भिन्नों, असमान भिन्नों, मिश्रित संख्याओं या सामान्य भिन्नों से भिन्नों को जोड़ने और घटाने का तरीका जानने के लिए इन चरणों का पालन करें। यदि आप पहले से ही एक तरीका जानते हैं, तो अन्य भिन्नों को हल करना वास्तव में आसान है!
कदम
विधि 1 का 4: समान भाजक के साथ भिन्नों को जोड़ना और घटाना
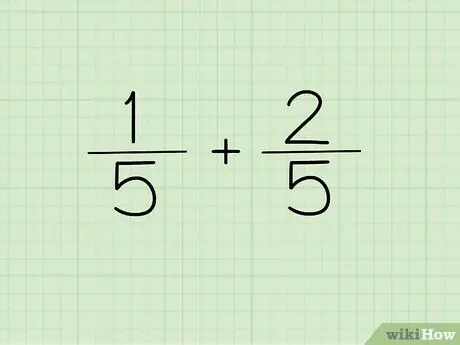
चरण 1. अपना प्रश्न लिखें।
यदि आप जिन दो भिन्नों को जोड़ना या घटाना चाहते हैं, उनका हर समान है, तो अपने उत्तर के हर के रूप में हर को एक बार लिख लें।
दूसरे शब्दों में, 1/5 और 2/5 को 1/5 + 2/5 = ?, लेकिन (1+2)/5 = के रूप में लिखा जा सकता है?. भाजक समान हैं, इसलिए उन्हें केवल एक बार लिखा जा सकता है। दो अंश संयुक्त हैं।
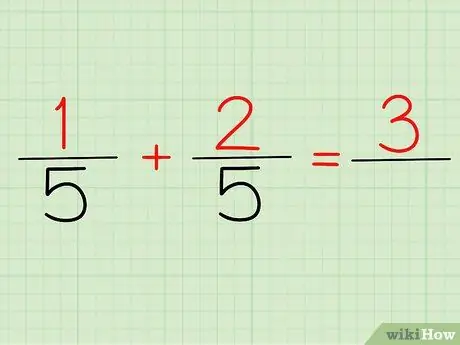
चरण 2. अंशों को जोड़ें।
अंश वह संख्या है जो किसी भिन्न के ऊपर होती है। यदि हम उपरोक्त समस्या को देखें, तो 1/5 और 2/5, 1 और 2 हमारे अंश हैं।
चाहे आप इसे 1/5 + 2/5 लिखें या (1+2)/5, आपका उत्तर वही होगा: 3! क्योंकि, 1 + 2 = 3

चरण 3. हर छोड़ दो।
चूँकि हर समान है, हर के साथ कुछ मत करो! जोड़ें, घटाएं, गुणा या भाग न करें। जाने भी दो।
तो, उसी उदाहरण से, हमारा हर 5 है। ठीक है! 5 हमारे भिन्न की निचली संख्या है। हमें आधा जवाब मिल गया है

चरण 4. अपना उत्तर लिखिए।
अब, आपको बस अपना अंश और हर लिख देना है! यदि आप ऊपर दिए गए उदाहरण का उपयोग करते हैं, तो आपका उत्तर 3/5 होगा।
आपका अंकगणित क्या है? 3. आपका हर? 5. इसलिए, 1/5 + 2/5 या (1+2)/5 बराबर है 3/5.
विधि 2 का 4: भिन्न भिन्नों के साथ भिन्नों को जोड़ना और घटाना

चरण 1. सबसे छोटा आम भाजक ज्ञात कीजिए।
अर्थात्, दोनों भिन्नों के लिए सबसे छोटा हर समान है। मान लीजिए कि हमारे पास भिन्न 2/3 और 3/4 हैं। भाजक क्या है? 3 और 4. दोनों भिन्नों का न्यूनतम उभयनिष्ठ भाजक ज्ञात करने के लिए, आप इसे तीन तरीकों से कर सकते हैं:
- के गुणज लिखिए। 3 के गुणज 3, 6, 9, 12, 15, 18… इत्यादि हैं। 4 के गुणज? 4, 8, 12, 16, 20, इत्यादि। वह छोटी से छोटी संख्या कौन सी है जो दोनों का गुणज हो? 12! वह सबसे कम आम भाजक है।
-
प्रधानीय कारन निकालना । यदि आप कारकों के बारे में जानते हैं, तो आप अभाज्य गुणनखंडन कर सकते हैं। यही है, आप उन संख्याओं की तलाश कर रहे हैं जो आपके हर को बनाते हैं। संख्या 3 के लिए गुणनखंड 3 और 1 हैं। संख्या 4 के गुणनखंड 2 और 2 हैं। फिर, आप सभी। 3 x 2 x 2 = 12. आपका सबसे छोटा उभयनिष्ठ हर!
छोटी संख्या के लिए सभी संख्याओं को गुणा करें। कुछ समस्याओं में, इस तरह, आप दोनों संख्याओं को गुणा कर सकते हैं – 3 x 4 = 12. हालाँकि, यदि आपके पास एक बड़ा हर है, तो ऐसा न करें! आप ५६ x ४४ को गुणा नहीं करना चाहते हैं और २,४६४ प्राप्त करने के लिए पूरी तरह से बाहर जाना चाहते हैं

चरण 2. हर में सबसे छोटा सामान्य हर प्राप्त करने के लिए आवश्यक संख्या से गुणा करें।
दूसरे शब्दों में, आप चाहते हैं कि आपके सभी हर बराबर हों। हमारे उदाहरण में, हम चाहते हैं कि हर 12 हो। 3 से 12 बदलने के लिए, आप 3 को 4 से गुणा करते हैं। 4 से 12 को बदलने के लिए, आप 4 को 3 से गुणा करते हैं। वही हर आपके अंतिम उत्तर का हर होगा।
-
तो 2/3 2/3 x 4 हो जाता है और 3/4 3/4 x 3 हो जाता है। यानी अब हमारे पास 2/12 और 3/12 है। लेकिन, हम अभी तक नहीं हुए हैं!
- आप देखेंगे कि हरों को एक दूसरे से गुणा किया जाता है। यह इस स्थिति में किया जा सकता है, लेकिन सभी स्थितियों में नहीं। कभी-कभी, दोनों हरों को गुणा करने के बजाय, आप छोटी संख्या प्राप्त करने के लिए दोनों हरों को दूसरी संख्या से गुणा कर सकते हैं।
- फिर अन्य समस्याओं में, कभी-कभी आपको समस्या में दूसरे भिन्न के हर के बराबर बनाने के लिए बस एक हर को गुणा करने की आवश्यकता होती है।

चरण 3. अंश को उसी संख्या से गुणा करें।
जब आप हर को किसी संख्या से गुणा करते हैं, तो आपको अंश को भी उसी संख्या से गुणा करना होगा। अंतिम चरण में हमने जो किया वह गुणन का केवल एक हिस्सा है जिसे करना है।
हमारे पास पहले चरण के रूप में 2/3x4 और 2/4x3 हैं - फिर, दूसरे चरण में, 2 x 4/3 x 4 और 3 x 3/4 x 3। यानी हमारे नए नंबर 8/12 और 9/ हैं। 12. उत्तम
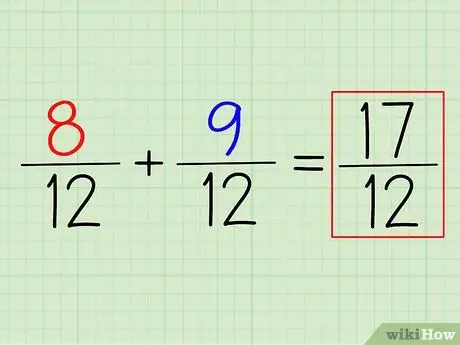
चरण 4. उत्तर पाने के लिए अंशों को जोड़ें (या घटाएं)।
8/12 + 9/12 जोड़ने के लिए, आपको केवल अंशों को जोड़ना है। याद रखें: बस हर को छोड़ दें। आपके द्वारा पाया जाने वाला सबसे छोटा आम भाजक आपका अंतिम भाजक है।
इस उदाहरण में, (8+9)/12 = 17/12। इसे एक मिश्रित संख्या में बदलने के लिए, बस अंश से हर घटाएं और शेष को लिख लें। इस मामले में, 17/12 = 1 5/12।
विधि 3 का 4: मिश्रित और सामान्य भिन्नों को जोड़ना और घटाना
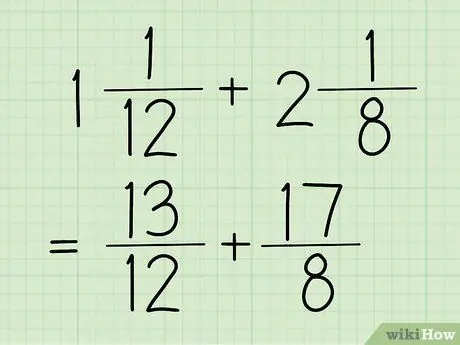
चरण 1. अपने मिश्रित भिन्नों को उभयनिष्ठ भिन्नों में बदलें।
एक मिश्रित संख्या एक भिन्न होती है जिसमें एक पूर्ण संख्या और एक भिन्न होती है, जैसा कि ऊपर दिए गए उदाहरण (1 5/12) में है। इस बीच, एक साधारण अंश एक भिन्न होता है जिसका अंश (शीर्ष संख्या) हर (निचला संख्या) से बड़ा होता है। यह अंश पिछले चरण में भी देखा जाता है, जो कि 17/12 है।
इस खंड के उदाहरणों के लिए, हम 13/12 और 17/8 का उपयोग करेंगे।

चरण 2. एक सामान्य भाजक खोजें।
क्या आपको कम से कम सामान्य भाजक खोजने के तीन तरीके याद हैं? गुणकों को लिखकर, अभाज्य गुणनखंडन का उपयोग करके, या हरों को गुणा करके।
आइए हमारे उदाहरण 12 और 8 के गुणज ज्ञात करें। वह सबसे छोटी संख्या कौन सी है जो दोनों में समान है? 24. 8, 16, 24, और 12, 24 - बिंगो

चरण 3. तुल्य भिन्न ज्ञात करने के लिए अपने अंश और हर को गुणा करें।
दोनों हर को 24 में बदलना होगा। आप 12 को 24 में कैसे बदलते हैं? 2. 8 से 24 गुणा करें? तीन से गुणा करें। लेकिन मत भूलो - आपको अंशों को भी गुणा करना होगा!
तो (13 x 2)/(12 x 2) = 26/24। और (17 x 3)/(8 x 3) = 51/24। हम इसे लगभग पूरा कर चुके हैं

चरण 4. अपने भिन्नों को जोड़ें या घटाएं।
अब जब आपके पास एक ही हर है, तो आप आसानी से दो अंशों को एक साथ जोड़ सकते हैं। याद रखें, बस हर को छोड़ दें!
26/24 + 51/24 = 77/24। वह आपकी राशि है! हालाँकि, शीर्ष पर संख्या बहुत बड़ी थी …

चरण 5. अपने उत्तर को वापस मिश्रित संख्याओं में बदलें।
भिन्न के शीर्ष पर बहुत बड़ी संख्या थोड़ी अजीब लगती है - आप अपने अंश का आकार नहीं बता सकते। आपको बस इतना करना है कि अपने हर को अंश से बार-बार घटाना है जब तक कि इसे और घटाया नहीं जा सकता है और शेष को लिख लें।
-
इस उदाहरण में, 77 घटा 24 गुणा 3 गुना। यानी 24 x 3 = 72. शेषफल 5 है! तो आपका अंतिम परिणाम क्या है? 3 5/24.
सच है!
विधि 4 का 4: एलसीएम ज्ञात किए बिना भिन्नों को जोड़ें और घटाएं
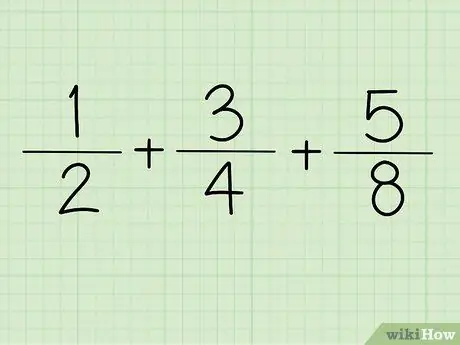
चरण 1. भिन्न लिखिए।
उदाहरण के लिए + +

चरण 2. पहले अंश को हल करें।
- दूसरे भिन्न के अंश से गुणा करें।
- 1 को 4 और 8 से गुणा करें। [32]
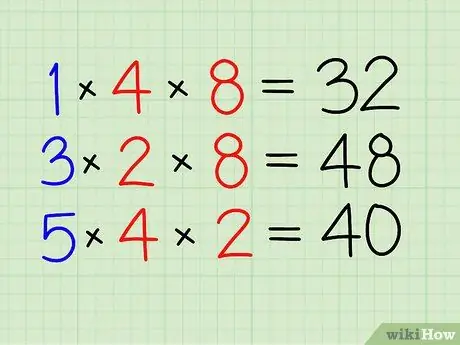
चरण 3. अन्य भिन्नों के लिए भी ऐसा ही करें।
- 3 को 2 और 8 से गुणा करें। [48]
- अंत में, 5 को 4 और 2 से गुणा करें। [40]
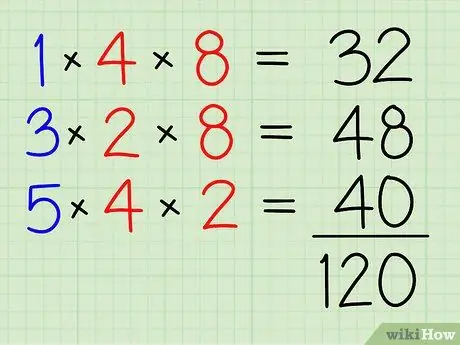
चरण 4. उन सभी को एक साथ जोड़ें।
32+48+40=120
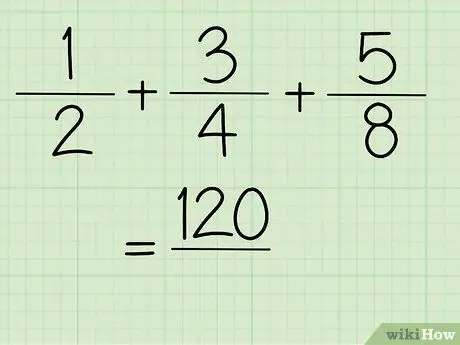
चरण 5. अब, आपको अंश मान प्राप्त होता है।

चरण 6. भिन्न के हर को हल करें।

चरण 7. सभी भिन्नों के हरों को गुणा करें।
2×4×8=64

चरण 8. अब, आप परिणाम प्राप्त करें।
120/64 = 1 56/64 = 1 ⅞
चेतावनी
- यह विधि आपको बड़ी संख्या में गुणा करने की अनुमति देती है।
- इस तरह से गणना करने के लिए आपको एक कैलकुलेटर की आवश्यकता हो सकती है।







